复杂度分析
复杂度分析犹如浩瀚的算法宇宙中的时空向导,它带领我们在时间与空间这两个维度上深入探索,寻找更优雅的解决方案。
算法效率评估
在算法设计中,我们先后追求以下两个层面的目标:
- 找到问题解法:算法需要在规定的输入范围内,可靠地求得问题的正确解。
- 寻求最优解法:同一个问题可能存在多种解法,我们希望找到尽可能高效的算法。
也就是说,在能够解决问题的前提下,算法效率已成为衡量算法优劣的主要评价指标,它包括以下两个维度。
- 时间效率:算法运行速度的快慢。
- 空间效率:算法占用内存空间的大小。
效率评估方法主要分为两种:实际测试、理论估算。由于实际测试具有较大的局限性,我们可以考虑仅通过一些计算来评估算法的效率。这种估算方法被称为「渐近复杂度分析 asymptotic complexity analysis」,简称「复杂度分析」。
复杂度分析体现算法运行所需的时间(空间)资源与输入数据大小之间的关系。它描述了随着输入数据大小的增加,算法执行所需时间和空间的增长趋势。
复杂度分析克服了实际测试方法的弊端,体现在以下两个方面:
- 它独立于测试环境,分析结果适用于所有运行平台。
- 它可以体现不同数据量下的算法效率,尤其是在大数据量下的算法性能。
时间复杂度
时间复杂度分析统计的不是算法运行时间,而是算法运行时间随着数据量变大时的增长趋势。
设输入数据的大小为n,则常见的时间复杂度类型如下:
常数阶O(1) < 对数阶O(logn) < 线性阶O(n) < 线性对数阶O(nlogn) < 平方阶O(n²) < 指数阶O(2ⁿ) < 阶乘阶O(n!)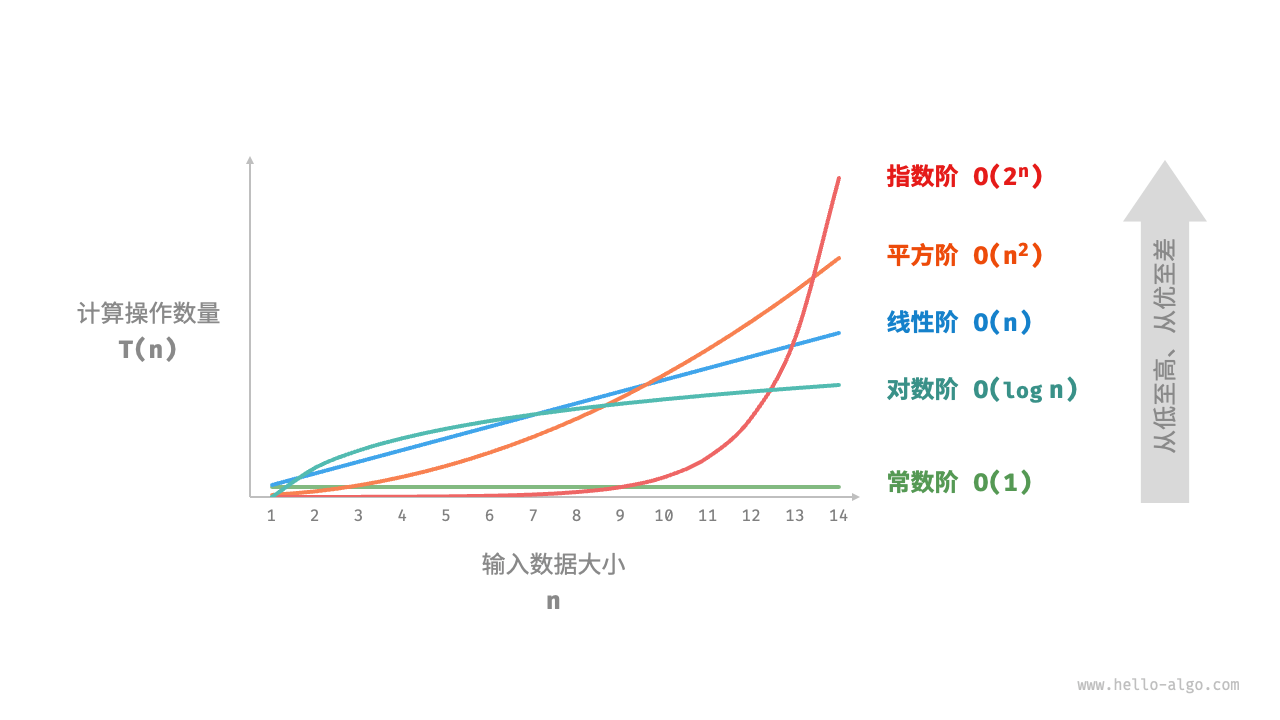
常数阶O(1)
// tips: 数量10000很大,但跟输入量n无关,依然为常数阶O(1)
const constant = () => {
for (let i = 0; i < 10000; i++) {
console.log(i);
}
}
对数阶O(logn)
// tips:对数阶常见特性是:每轮缩减一半
const logarithmic = (n) => {
let count = 0;
while(n > 1) {
n = n / 2;
count++;
}
return count;
}
线性阶O(n)
// tips: 线性阶通常所输入量n线性增长,通常出现在单层遍历中。
const linear = (n) => {
let count = 0;
for (let i = 0; i < n; i++) {
count++;
}
return count;
}
线性对数阶O(nlogn)
// tips: 线性对数阶常出现于嵌套循环中,两层循环的时间复杂度分别为O(logn)和O(n)
const linearLogRecur = (n) => {
if (n <= 1) {
return 1;
}
let count = linearLogRecur(n / 2) + linearLogRecur(n / 2);
for (let i = 0; i < n; i++) {
count++;
}
return count;
}
平方阶O(n²)
// tips: 平方阶通常出现在嵌套循环中,其中两层循环的时间复杂度都为O(n)
const quadratic = (n) => {
let count = 0;
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
count++;
}
}
return count;
}
指数阶O(2ⁿ)
// tips: 生物学中“细胞分裂”就是一个典型的指数阶案例,一生二,二生四...
const exponential = (n) => {
let count = 0;
let base = 1;
for (let i = 0; i < n; i++) {
for (let j = 0; j < base; j++) {
count++;
}
base = base * 2
}
// 1 + 2 + 4 + ....+ 2^(n - 1) = 2^n - 1
return count;
}
阶乘阶O(n!)
// tips: 阶乘阶对应数学中的“全排列”问题:给定n个不重复的元素,求其所有可能的排列组合。
// 公式:n! = n * (n - 1) * (n - 2) * ..... * 2 * 1
const factorialRecur = (n) => {
if (n === 1) {
return 1;
}
let count = 0;
for (let i = 0; i < n; i++) {
count += factorialRecur(n - 1);
}
return count;
}
空间复杂度
空间复杂度用于衡量算法占用内存空间随着数据量变大时的增长趋势,这个概念与时间复杂度非常类似,只需将“运行时间”替换为“占用内存空间”。
设输入数据的大小为n,则常见的空间复杂度类型如下: 常数阶O(1) < 对数阶O(logn) < 线性阶O(n) < 平方阶O(n²) < 指数阶O(2ⁿ)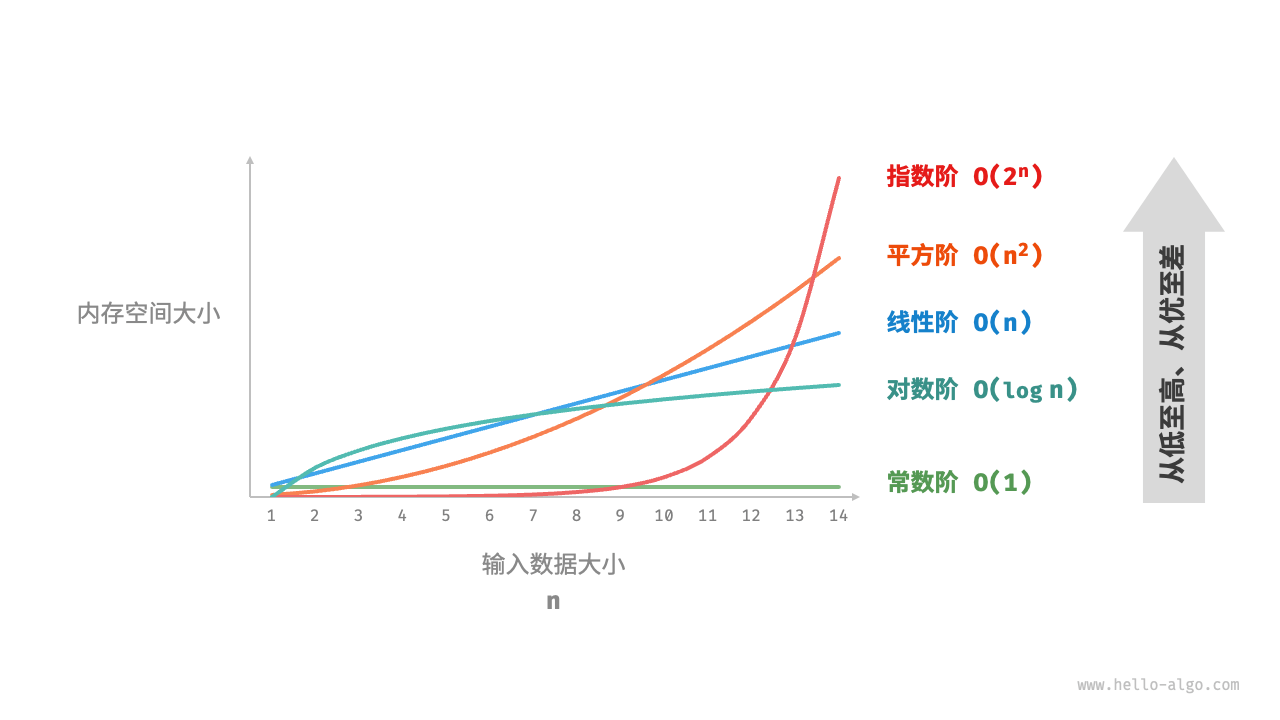
常数阶O(1)
// tips: 常数阶通常用于表示与输入量无关的常量,变量和对象的定义
const constant = (n) => {
let count = 1;
const array = new Array(100);
const obj = {};
// 省略其他
}
对数阶O(logn)
对数阶常见与分治算法中。例如归并排序,输入长度为n的数组,每轮递归将数组从中点划分为两半,形成高度为logn的递归树,使用O(logn)栈帧空间。
线性阶O(n)
// tips: 线性阶常见于元素数量与n成正比的数组、链表、栈、队列等
const linear = (n) => {
const array = new Array(n);
const set = new Set();
for (let i = 0; i < n; i++) {
set.add(i);
}
}
平方阶O(n²)
// tips: 平方阶常见于矩阵和图,元素数量与n成平方关系
const quadratic = (n) => {
const matrix = new Array(n).fill(0).map(() => new Array(n).fill(0))
return matrix
}
指数阶O(2ⁿ)
// tips: 常见与二叉树结构中
// 公式:2º + 2¹ + 2² + ... +2ⁿ﹣¹ = 2ⁿ - 1
const buildTree = (n) => {
if (n === 0) {
return null;
}
const root = new TreeNode(0);
root.left = buildTree(n - 1);
root.right = buildTree(n - 1);
return root;
}