分治

分治算法

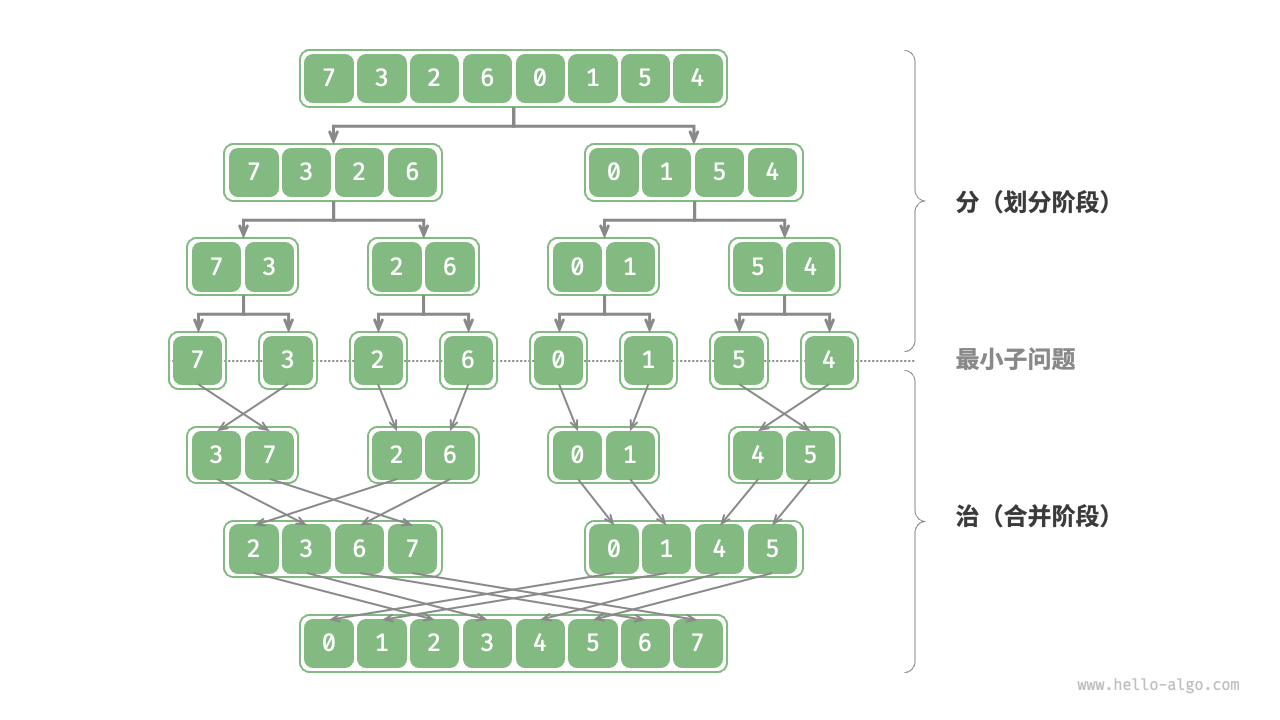
分治(Divide And Conquer)：全称分而治之，是一种非常重要且常见的算法策略。分治通常基于递归实现，包括以下两个步骤：

• 分(划分阶段)：递归的将原问题分解为两个或者多个子问题，直至到达最小问题时终止。
• 治(合并阶段)：从已知解的最小问题开始，从底至顶地将问题的解进行合并，从而构建出原问题的解。

如何判断分治问题

• 问题可以分解：原问题可以分解称规模更小、类似的子问题，以及能够以相同的方式进行递归。
• 子问题是独立的：子问题之间没有重叠，互补依赖，可以独立解决。
• 子问题的解可以合并：原问题的解通过合并子问题的解得来。

分治常见应用

• 常见算法：寻找最近点对、大整数乘法(例如Karatsuba)、矩阵乘法(例如Strassen)、汉诺塔问题、求解逆序对。
• 常见算法和数据结构：二分查找、归并排序、快速排序、桶排序、树、堆、哈希表。

分治搜索策略

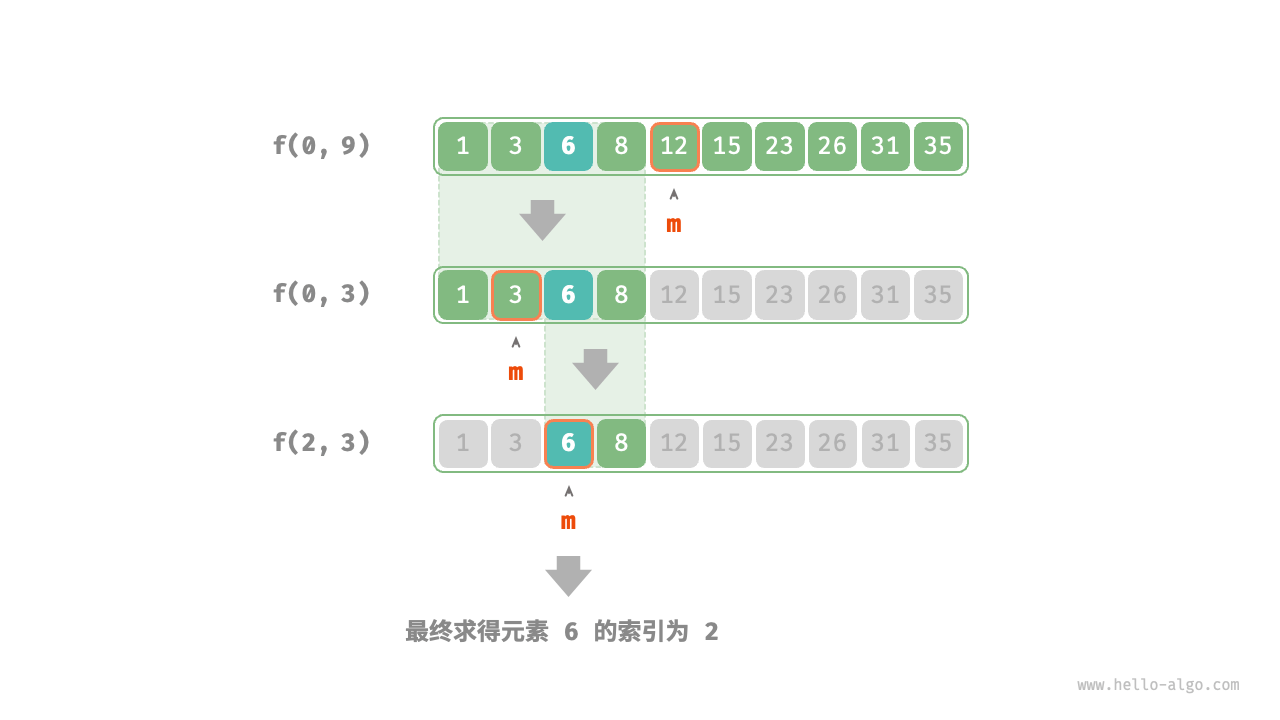
基于分治思想，实现二分查找：将搜索区间标记为[i, j]，对应的子问题标记为f(i, j)，以原问题f(0, n - 1)为起始点，通过以下步骤实现二分查找：

1. 计算搜索区间[i, j]的中点m，根据它排除一半的搜索区间。
2. 递归求解规模减小一半的子问题，可能为f(i, m - 1)或f(m + 1, j)。
3. 循环以上两步，直至找到target目标元素或者搜索区间为空。

function dfs(nums, target, i, j) {
  // 区间为空
  if (i > j) {
    return -1;
  }
  const mid = i + ((j - i) >> 1);
  if (nums[mid] < target) {
    return dfs(nums, target, mid + 1, j);
  } else if (nums[mid] > target) {
    return dfs(nums, target, i, mid - 1);
  } else {
    return mid;
  }
}
function binarySearchRecursion(nums, target) {
  const len = nums.length;
  return dfs(nums, target, 0, len - 1);
}

构建树问题

假设给定一棵二叉树的前序遍历(preOrder)和中序遍历(inOrder)，请从中构建二叉树，返回二叉树的根节点(假设二叉树中没有重复节点)。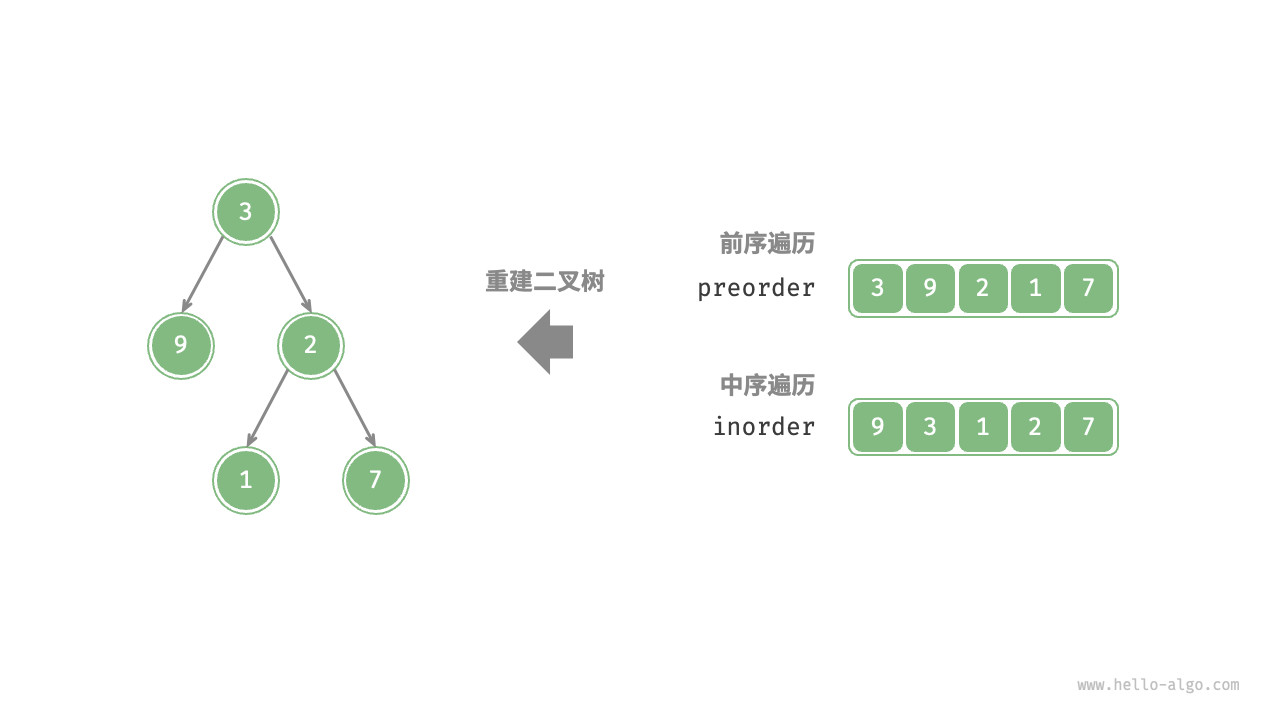

判断是否为分治问题

• 问题可以分解：从分治角度切入，我们可以将原问题划分为两个子问题和一个初始化操作：初始化根节点、构建左子树和构建右子树。对于每棵子树，任可以复用此步骤，直至到达空子树为止。
• 子问题是独立的：左子树和右子树相互独立，它们之间没有交集。
• 子问题的解是可以合并的：一旦得到了左子树和右子树，我们就可以将它们链接到根节点上，得到原问题的解。

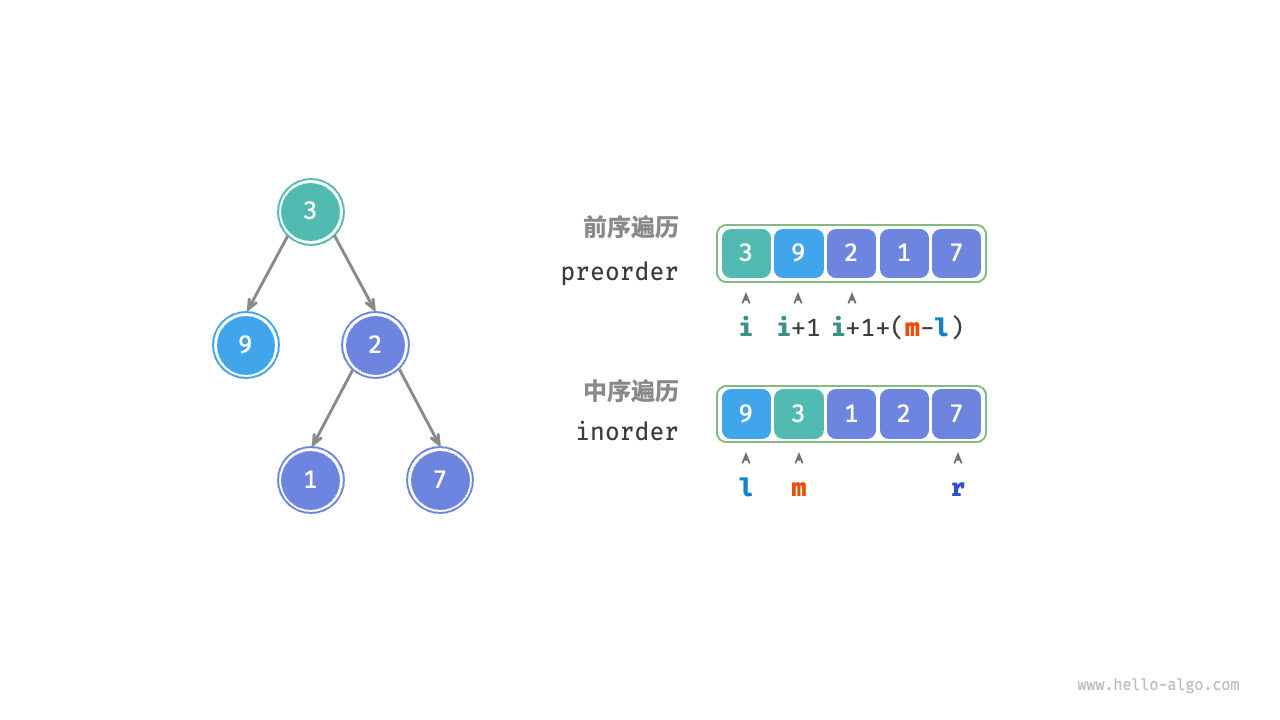
基于变量描述子树区间

• 将当前树的根节点在preOrder中的索引记为i。
• 将当前树的根节点在inOrder中的索引记为m。
• 当前树在inOrder中索引区间记为[l, r]。

根据以上变量即可表示根节点在preOrder中的索引以及子树在inOrder中的索引区间。

树	根节点在preOrder中的索引	子树在inOrder中的索引区间
当前树	i	[l, r]
左子树	i + 1	[l, m - 1]
右子树	i + 1 + (m - l)	[m + 1, r]

代码实现

// n为二叉树节点的数量
// 时间复杂度：O(n)
// 空间复杂度：O(n)
function dfs(preOrder, inOrderMap, i, l, r) {
  // 区间为空是，表示空子树，终止
  if (r - l < 0) {
    return null;
  }
  // 初始化根节点
  const rootVal = preOrder[i];
  const root = new TreeNode(rootVal);
  // 查询m，从而划分左、右子树
  const m = inOrderMap.get(rootVal);
  // 构建左子树
  root.left = dfs(preOrder, inOrderMap, i + 1, l, m - 1);
  // 构建右子树
  root.right = dfs(preOrder, inOrderMap, i + 1 + (m - l), m + 1, r);
  // 返回根节点
  return root;
}
function buildTree(preOrder, inOrder) {
  const inOrderLen = inOrder.length;
  const inOrderMap = new Map();
  for(let i = 0; i < inOrderLen; i++) {
    inOrderMap.set(inOrder[i], i);
  }
  const root = dfs(preOrder, inOrderMap, 0, 0,  inOrderLen - 1);
  return root;
}

汉诺塔问题

给定三根柱子，记为A、B和C。起始状态下A上套着N个圆盘，它们从上到下按照从小到大的顺序排列。我们的任务是要把这N个圆盘移动到柱子C上，并保持它们原有顺序不变，在移动圆盘的过程中，需要遵守以下规则。

1. 圆盘只能从一根柱子顶部拿出，从另一根柱子的顶部放入。
2. 每次只能移动一个圆盘。
3. 小圆盘必须时刻位于大圆盘之上。

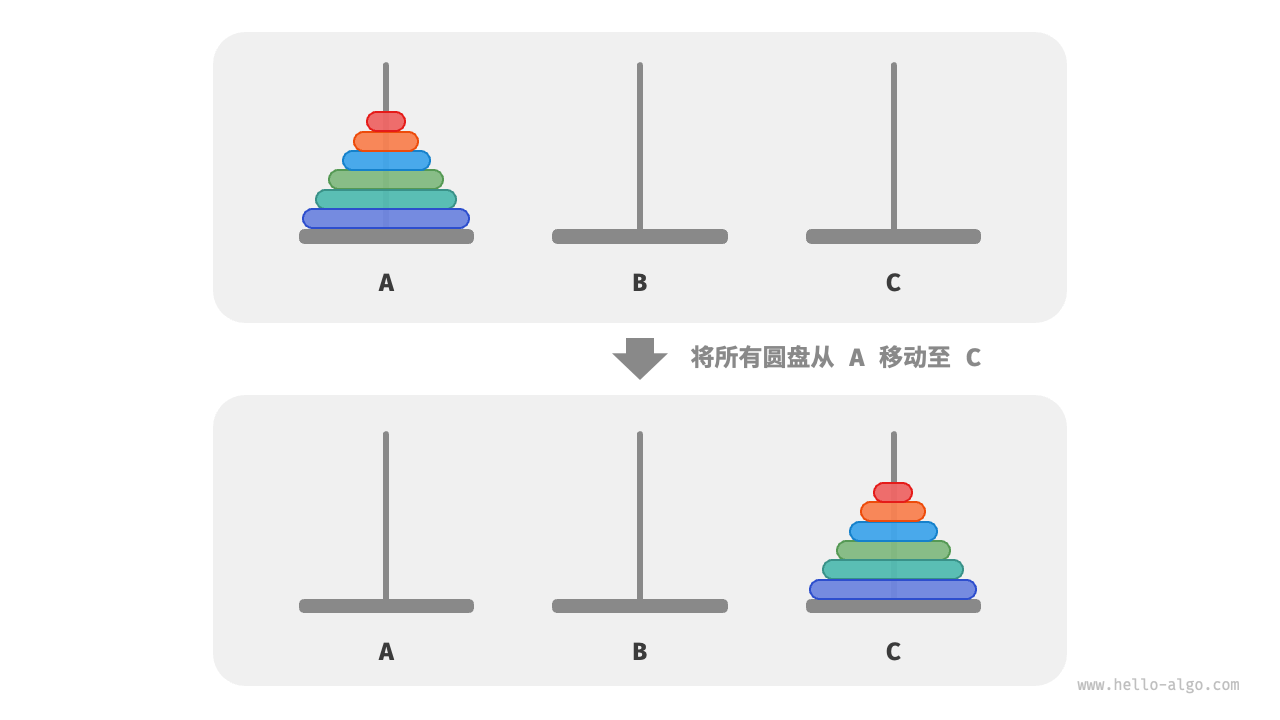
我们将规模为i的汉诺塔问题记作f(i)，例如：f(3)代表将3个圆盘从A移动到C。

基本情况

对于f(1)而言，只有一个圆盘，我们直接从A移动到C即可。

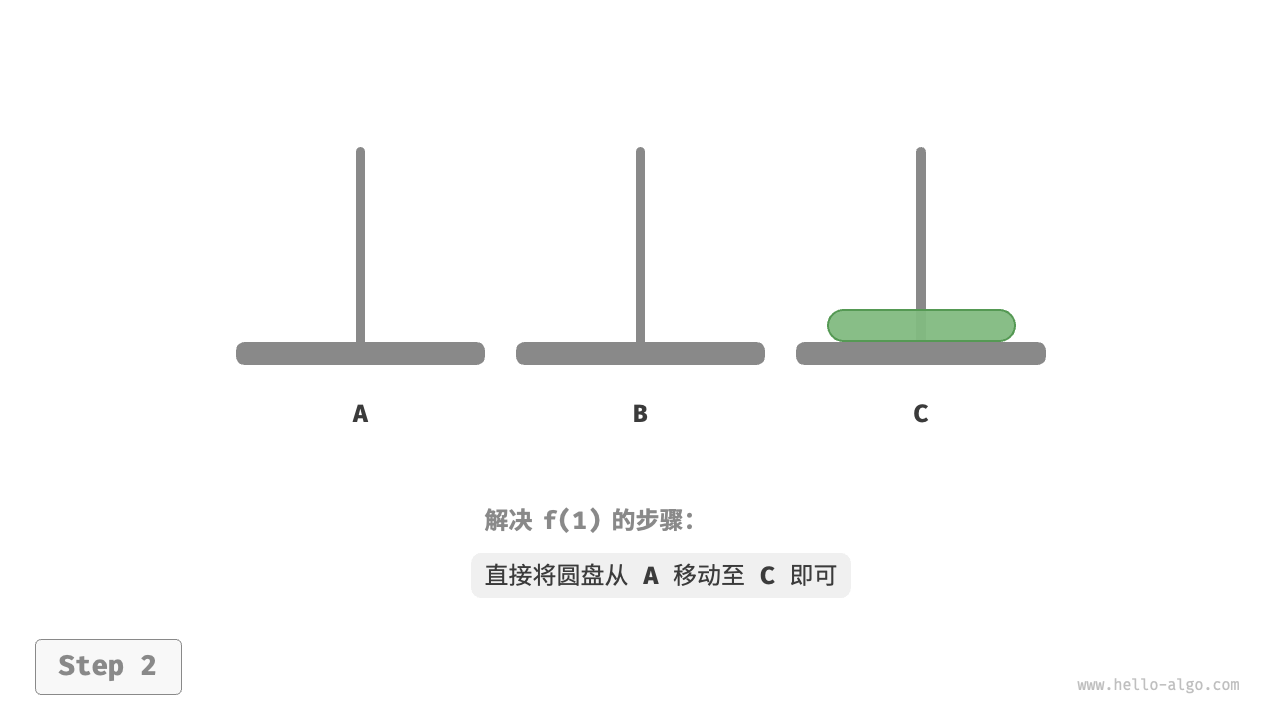
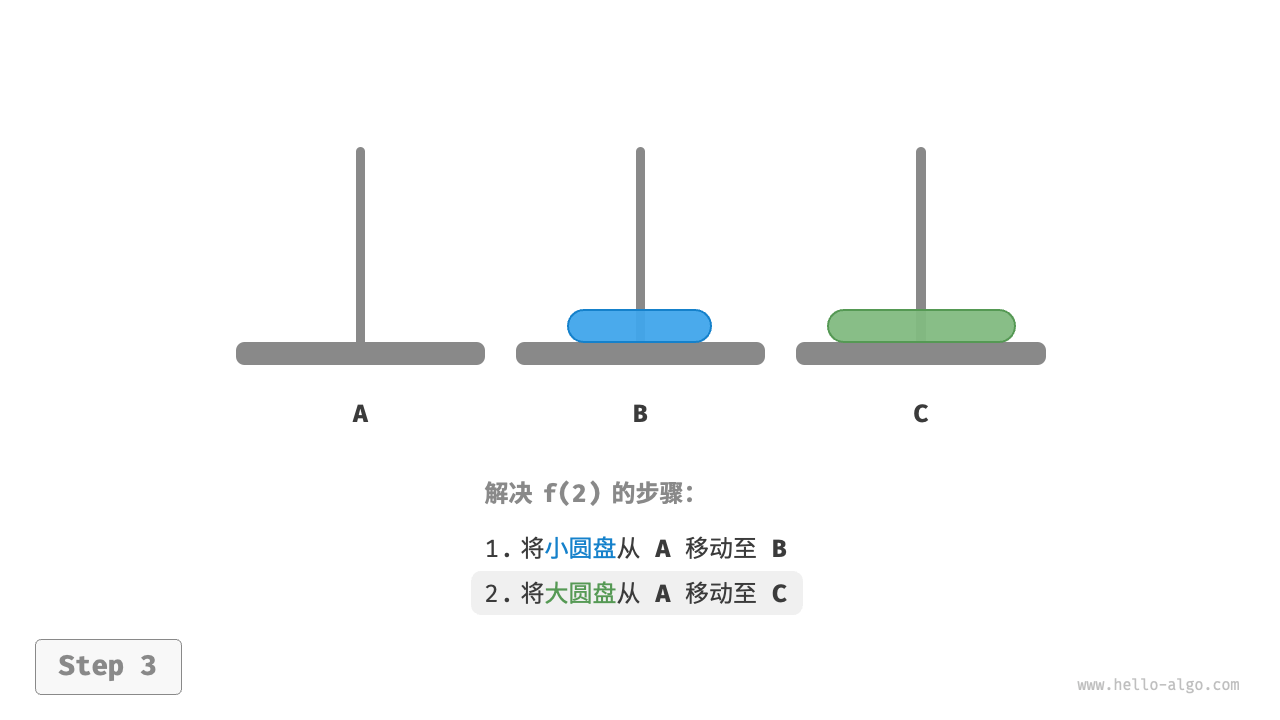
对于f(2)而言，需要遵守规则，借助B来完成移动：

1. 先将上面的小圆盘从A移至B。
2. 再将大圆盘从A移至C。
3. 最后将小圆盘从B移至C。

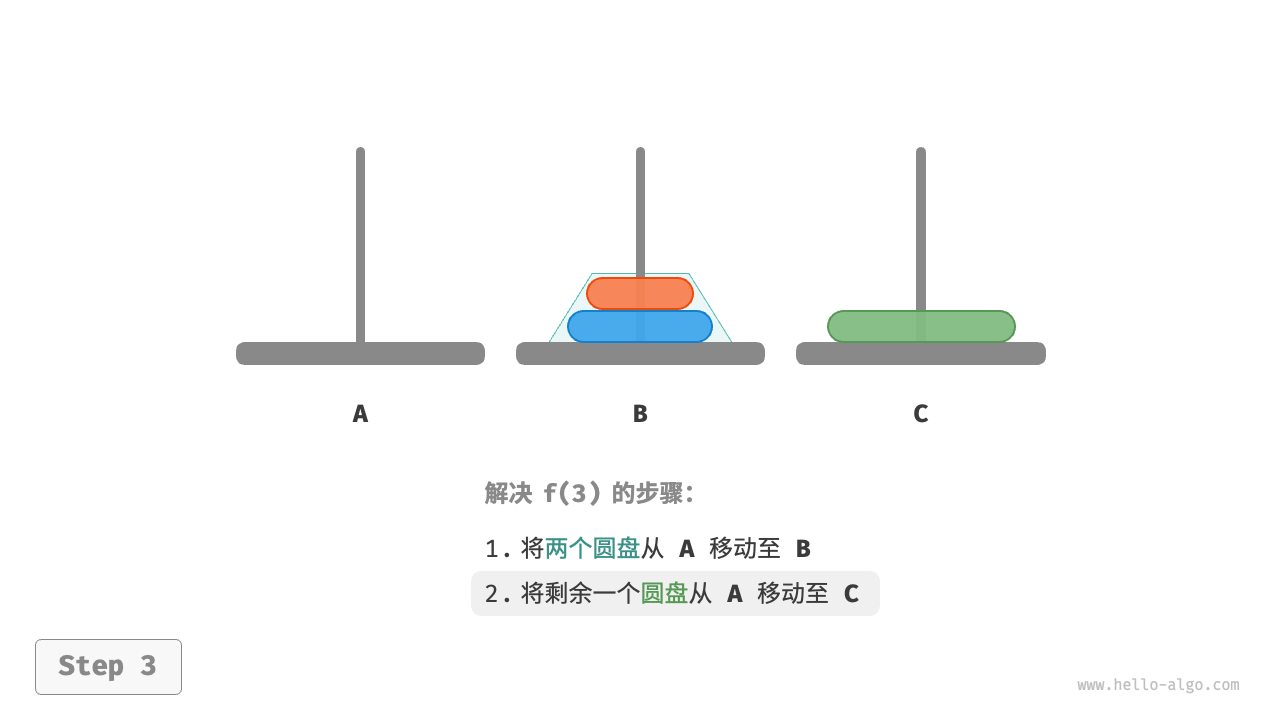
子问题分解

对于f(3)而言，因为已知f(1)和f(2)的解，所以我们可从分治角度思考：将A顶部的两个圆盘看做一个整体。

1. 令B为目标柱，C为缓冲柱，将两个圆盘从A移动到B。
2. 将A中剩余的一个圆盘从A直接移动到C。
3. 令C为目标柱，A为缓冲柱，将两个圆盘从B移动到C。

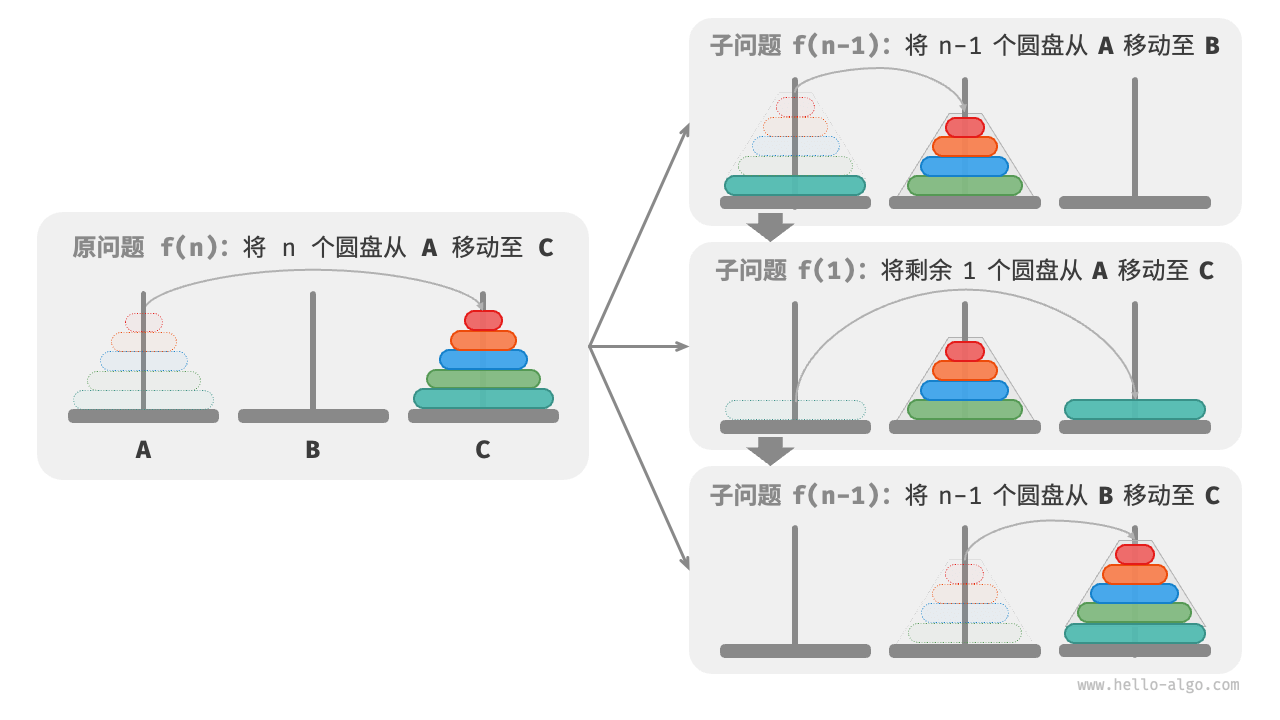
至此，我们总结出规律：将原问题f(n)划分为两个子问题f(n - 1)和f(1)，并按以下顺序解决这三个子问题。

1. 将n - 1个圆盘借助C从A移动至B。
2. 将剩余1个圆盘从A直接移动至C。
3. 将n - 1个圆盘借助A从B移动至C。

代码实现

function move(source, target) {
  // 从source柱顶部拿出一个圆盘
  const pan = source.pop();
  // 将圆盘放入target柱
  target.push(pan);
}
function dfs(i, source, buffer, target) {
  if (i === 1) {
    move(source, target);
    return;
  }
  // 子问题，从source上移动n - 1个圆盘到换buffer缓冲柱(借助target)
  dfs(i - 1, source, target, buffer);
  move(source, target);
  // 子问题，从buffer上移动n - 1个圆盘到target目标柱(借助source)
  dfs(i - 1, buffer, source, target);
}
function solveHanota(A, B, C) {
  const len = A.length;
  dfs(len, A, B, C);
}

参考

• Hello 算法 分治