动态规划

动态规划Dynamic Programming是一种重要的算法范式，它将一个问题分解为一系列更小的子问题，并通过存储子问题的解来避免重复计算，从而大幅提升时间效率。

初探动态规划

假设给定n个楼梯，每步只能1阶或者2阶，请问有多少种方案可以爬到楼顶？我们以n为3具体，具体爬楼梯过程如下图：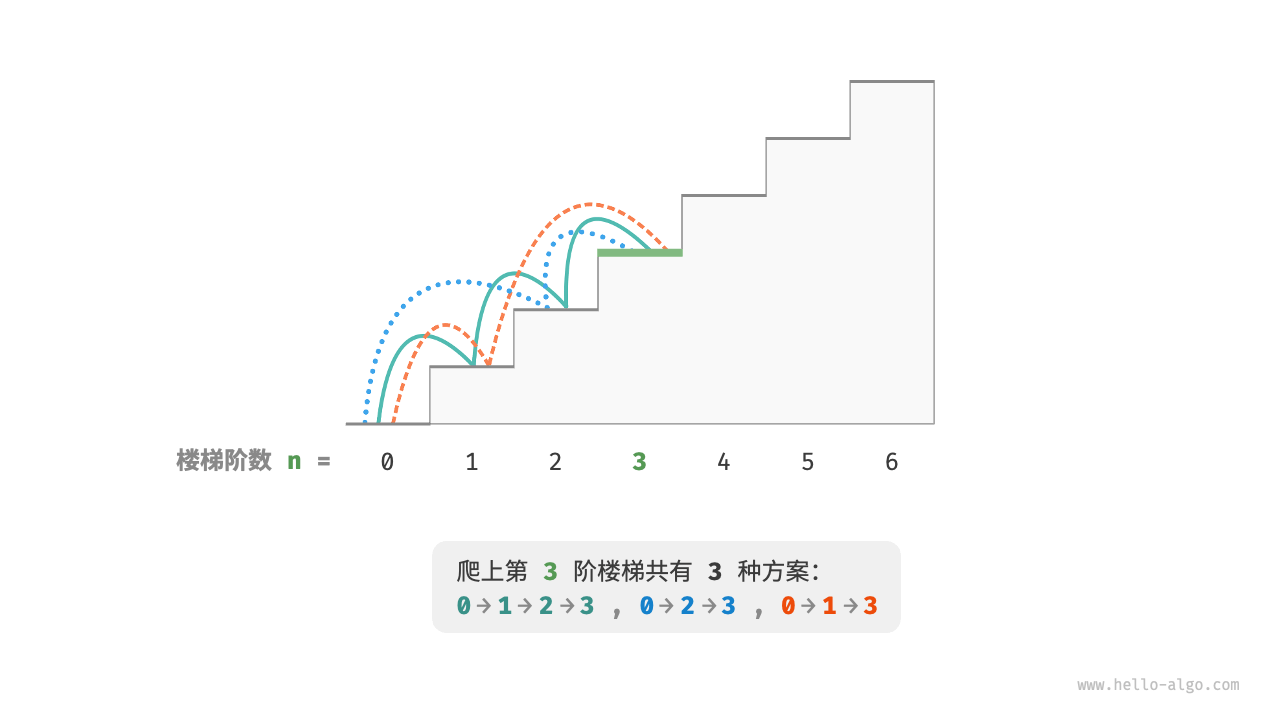

方法一：回溯

对于这一个问题，可以用上一节回溯算法来实现，其代码如下：

const backTracking = (state, n, choices, res) => {
  // 爬到第n个台阶，数量加1
  if (state === n) {
    res.set(0, res.get(0) + 1);
    return;
  }
  // 遍历所有选择
  for (const choice of choices) {
    // 剪枝：不允许超过n
    if(state + choice > n) {
      continue;
    }
    // 尝试：做出选择，更新状态
    backTracking(state + choice, n, choices, res);
    // 回退：无
  }
};
export default function climbingStairsBacktrack(n) {
  // 步骤选择
  const choices = [1, 2];
  // 从0阶开始爬
  const state = 0;
  // 存储最终结果
  const res = new Map();
  res.set(0, 0);

  backTracking(state, n, choices, res);
  return res.get(0);
}

方法二：暴力搜索

回溯算法通常并不显示的对问题进行拆解，而是将求解问题看做一系列决策步骤，通过试探和剪枝，搜索所有可能得解。

如果通过问题分解的角度来分析问题，可得到这样一个规律：爬到第i - 1阶的方案加上爬到第i - 2阶的方案就等于爬到第i阶的方案数，其公式为：dp[i] = dp[i - 1] + dp[i - 2]。

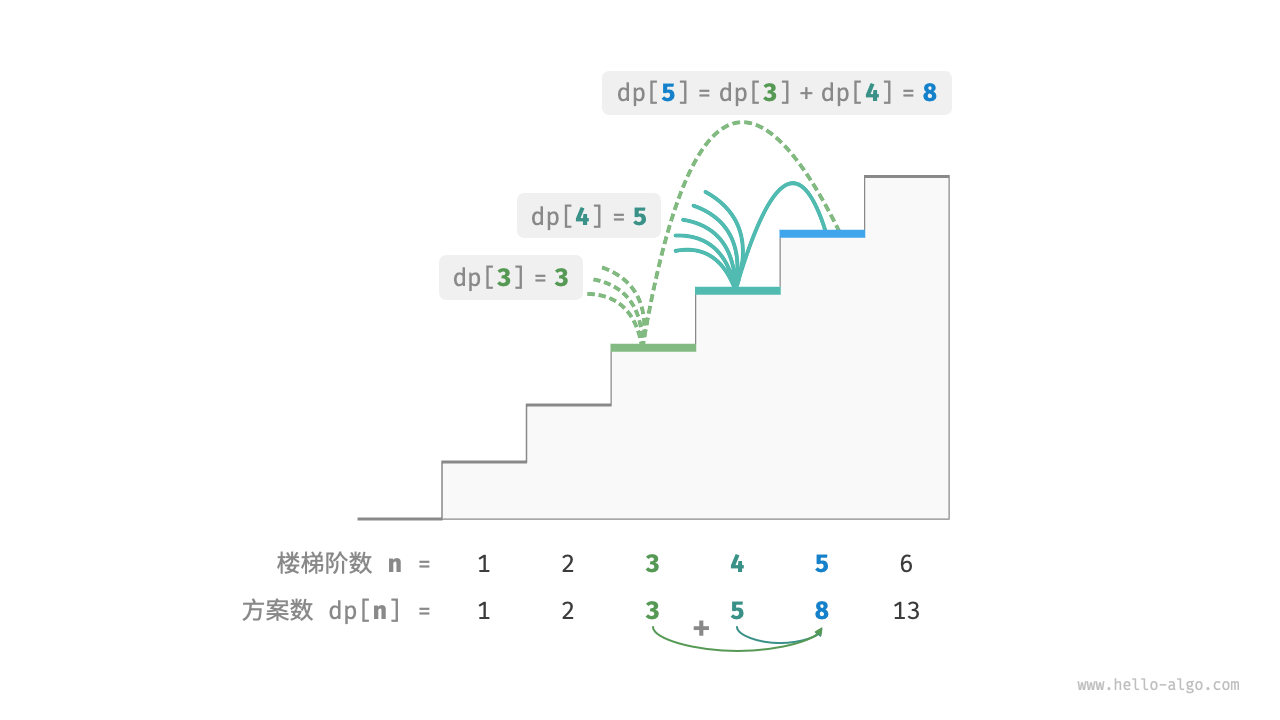
其实现代码如下：

const dfs = (n) => {
  if (n === 1 || n === 2) {
    return n;
  }
  const count = dfs(n - 1) + dfs(n - 2);
  return count;
};
export default function climbingStairsDFS(n) {
  return dfs(n);
}

方法三：记忆化搜索

对于暴力搜索解法，以n = 9为例，其分解图如下：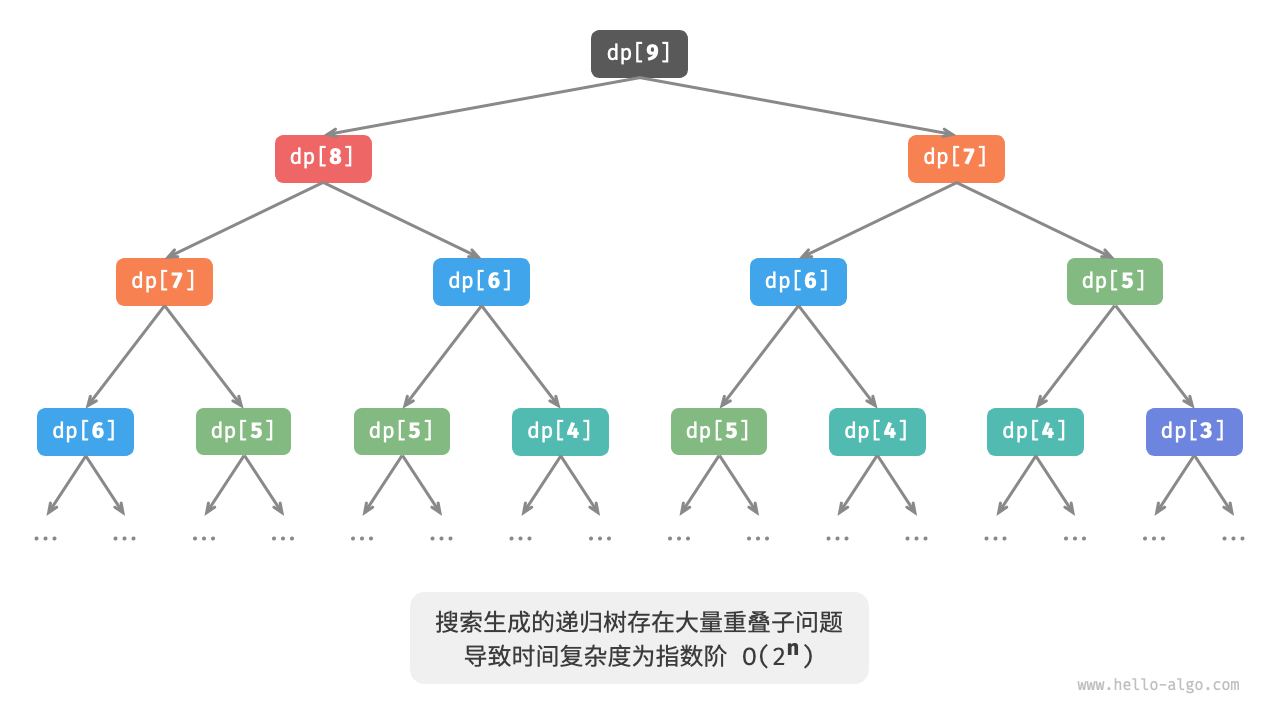

可以看到，暴力搜索形成的递归树，其递归深度为n，时间复杂度为O(2ⁿ)。指数阶属于爆炸式增长，如果我们输入一个比较大的数，则会陷入漫长的等待中。

通过观察，指数阶的时间复杂度是重叠子问题导致的，例如dp[9]被分解为dp[8]和dp[7]，而dp[8]又被分解为dp[7]和dp[6]，它们都包含子问题dp[7]。

为了解决以上问题，可通过引入记忆数组的方式来解决，其实现代码如下：

const dfsMember = (n, member) => {
  if (n === 1 || n === 2) {
    return n
  }
  if (member[n] !== -1) {
    return member[n]
  }
  const count = dfsMember(n - 1, member) + dfsMember(n - 2, member)
  member[n] = count
  return count
}
export default function climbingStairsDfsMember (n) {
  const member = new Array(n + 1).fill(-1)
  return dfsMember(n, member)
}

经过以上处理，实际分解子问题如下图所示：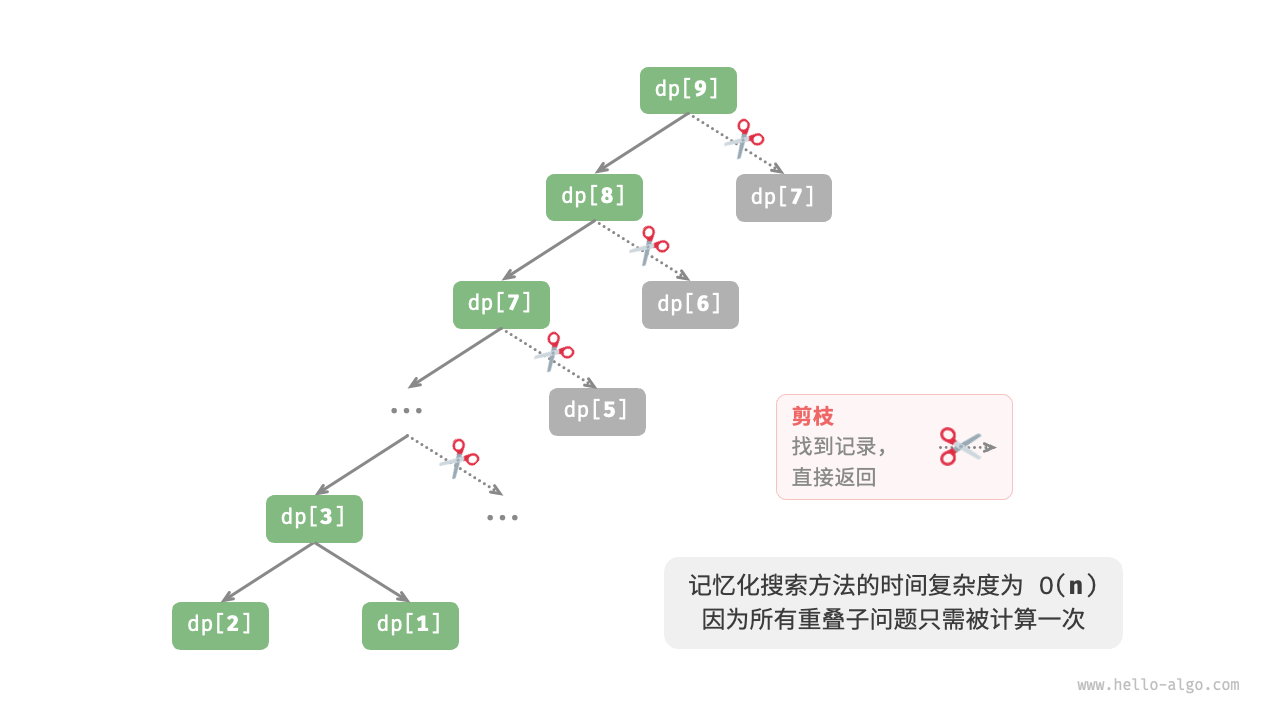

方法四：动态规划

记忆化搜索是一种从顶至底的方法：我们从原问题开始出发，递归的将较大的问题分解为较小的问题，直至解已知的最小子问题。之后，通过回溯层层收集问题的解，构建出原问题的解。

与之相反，动态规划是一种从底到顶的方法：从最小子问题的解开始，迭代地构建更大的子问题的解，直至得到原问题的解。

其实现代码如下：

export default function climbingStairsDP (n) {
  if (n === 1 || n === 2) {
    return n
  }
  // 初始化dp表
  const dp = new Array(n + 1).fill(-1)
  // 初始状态：预设最小问题的解
  dp[1] = 1
  dp[2] = 2
  // 状态转移：从较小子问题逐步求解较大子问题
  for(let i = 3; i <= n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2]
  }
  return dp[n]
}

根据以上代码可以发现：dp[i]至于dp[i - 1] + dp[i - 2]有关，因此无须定义dp数组，其空间优化代码如下：

export default function climbingStairsDP (n) {
  if (n === 1 || n === 2) {
    return n
  }
  // 初始状态：预设最小问题的解
  let a = 1
  let b = 2
  // 状态转移：从较小子问题逐步求解较大子问题
  for(let i = 3; i <= n; i++) {
    let temp = b
    b = a + b
    a = temp
  }
  return b
}

以上代码，使用图例表示如下：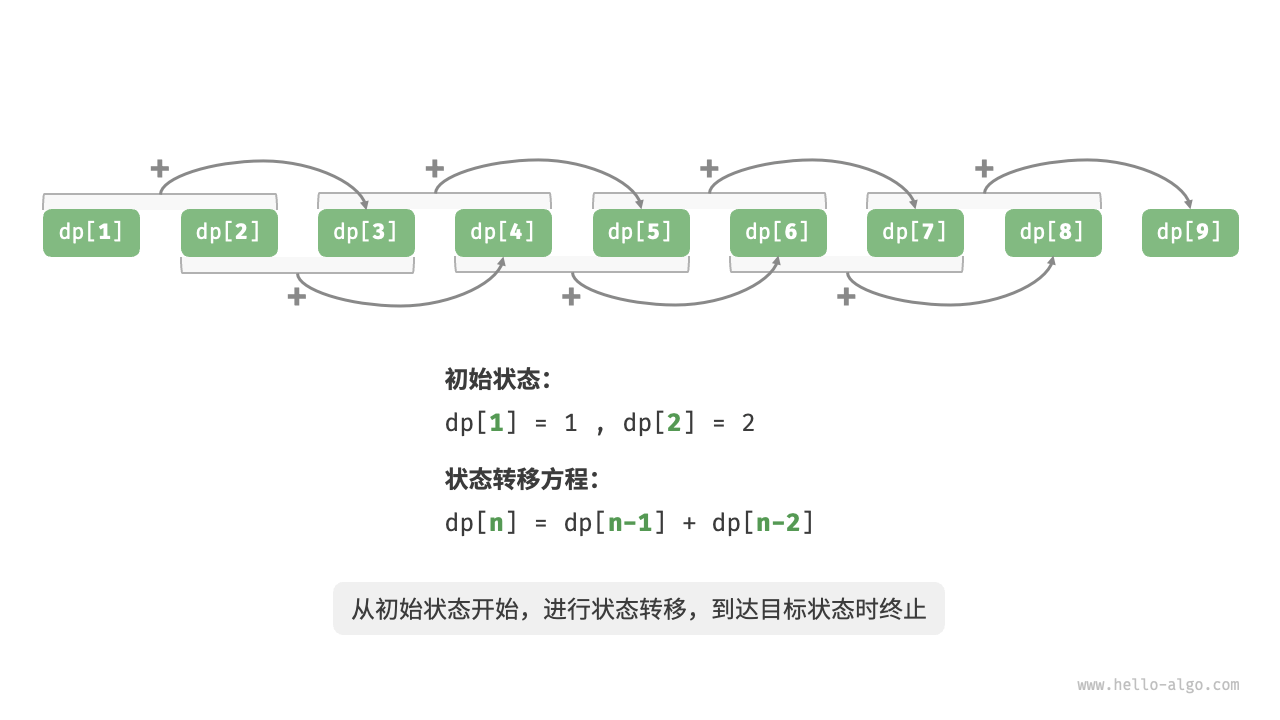

在动态规划中，有一些术语：

• dp表：例如以上代码中的dp数组。其中dp[i]被称为对应子问题的解。
• 初始状态：最小子问题对应的状态，例如以上代码中的1和2。
• 状态转移方程：以上代码中的递推公式：dp[i] = dp[i - 1] + dp[i - 2]。

DP问题特性

子问题分解是一种通用的算法思路，在分治，动态规划和回溯中的侧重点不同，如下：

• 分治算法：分治算法递归的将原问题划分为多个相互独立的子问题，直至最小子问题，并在回溯中合并子问题的解，最终得到原问题的解。
• 动态规划：动态规划也对问题进行分解，但与分治算法的主要区别是，动态规划中的子问题是相互依赖的，在分解过程中会出现许多重叠的子问题。
• 回溯算法：回溯算法在尝试和回退中穷举所有可能的解，并通过剪枝避免不必要的搜索分支。原问题的解由一系列决策步骤构成，可以将每个决策步骤之前的子序列看出一个子问题。

实际上，动态规划常用来求解最优化问题，它们不仅包含重叠子问题，还具有另外两大特性：最优子结构、无后效性。

最优子结构

最优子结构的含义：原问题的最优解是从子问题的最优解构建得来的。

假设有这样一个问题：给定一个楼梯，每步可以上1阶或者2阶，每一阶楼梯上都贴有一个非负整数，表示在该台阶所需要付出的代价。给定一个非负整数数组cost，其中cost[i]表示在第i个台阶需要付出的代价，cost[0]为地面(起始点)，请问最小需要付出多少代价才能到达顶部？

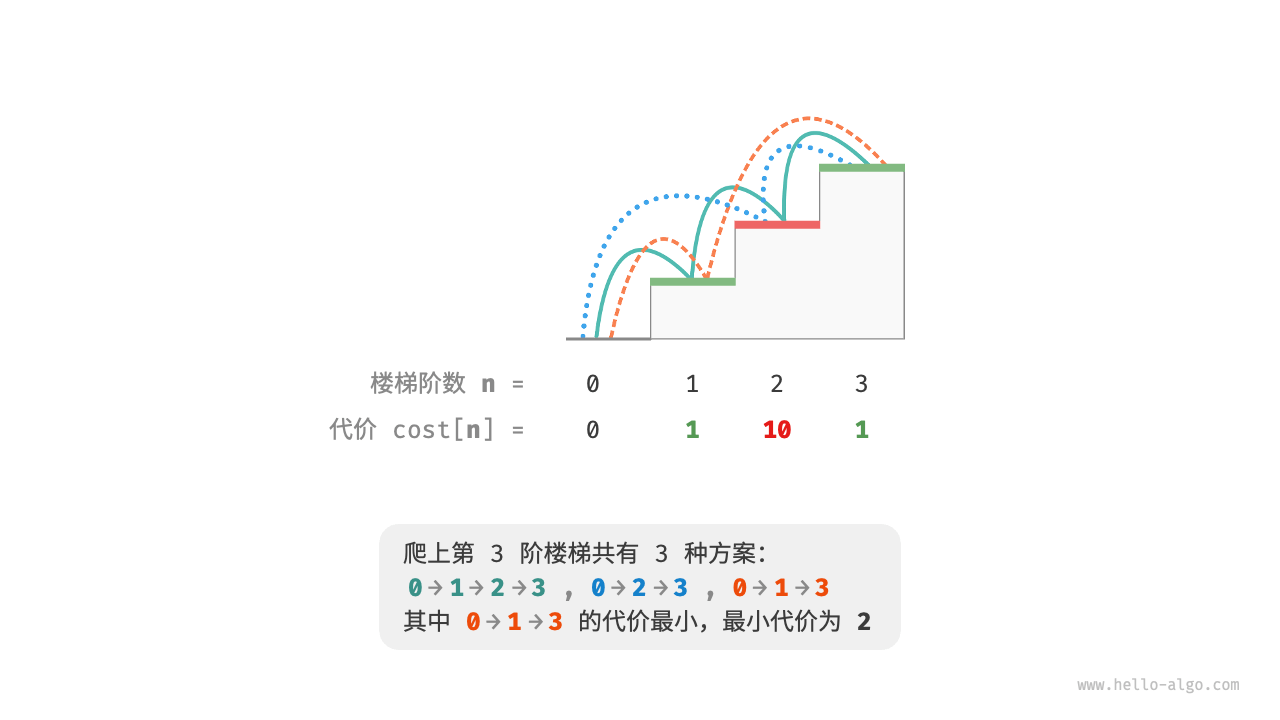
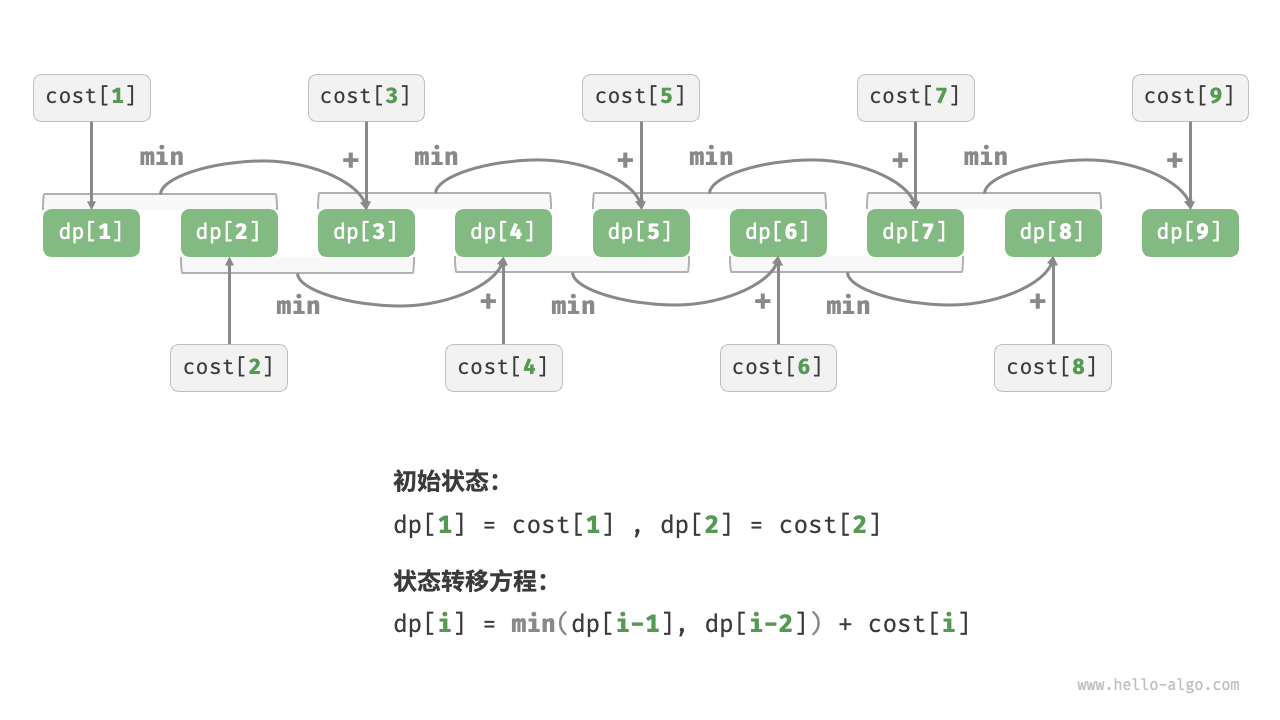
设dp[i]为爬到第i阶累计付出的代价，由于第i阶只能从i - 1或者i - 2阶走来，因此d[i]只可能等于dp[i - 1] + cost[i]或者dp[i - 2] + cost[i]。为了尽可能减少代价，应该选择两者中较小的那一个，其公式为：dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i]。

其实现代码如下：

export default function minCostClimbingStairsDP(cost) {
  const n = cost.length - 1;
  if (n === 1 || n === 2) {
    return cost[n];
  }
  // 初始状态：预设最小问题的解
  let a = cost[1];
  let b = cost[2];
  // 状态转移：从较小的子问题逐步求解较大子问题
  for(let i = 3; i <= n; i++) {
    let temp = b;
    b = Math.min(a, b) + cost[i];
    a = temp;
  }
  return b;
}

无后效性

无后效性：无后效性是动态规划能够有效解决问题的重要特性之一，其定义为：给定一个确定的状态，它的未来发展只与当前状态有关，而与过去的经历的所有状态无关。

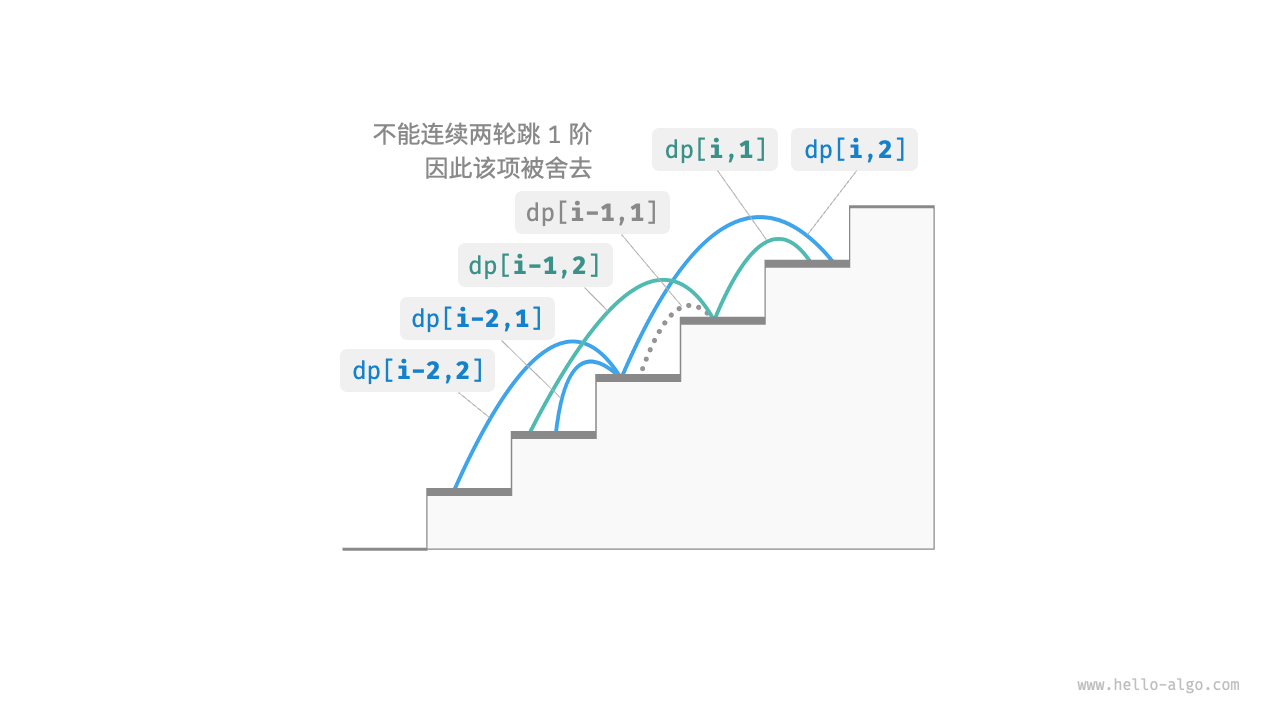
假设有这样一个问题：给定一个n阶的楼梯，每步可以上1阶或者2阶，但不能连续两轮跳1阶，请问有多少种方案可以爬到楼顶？

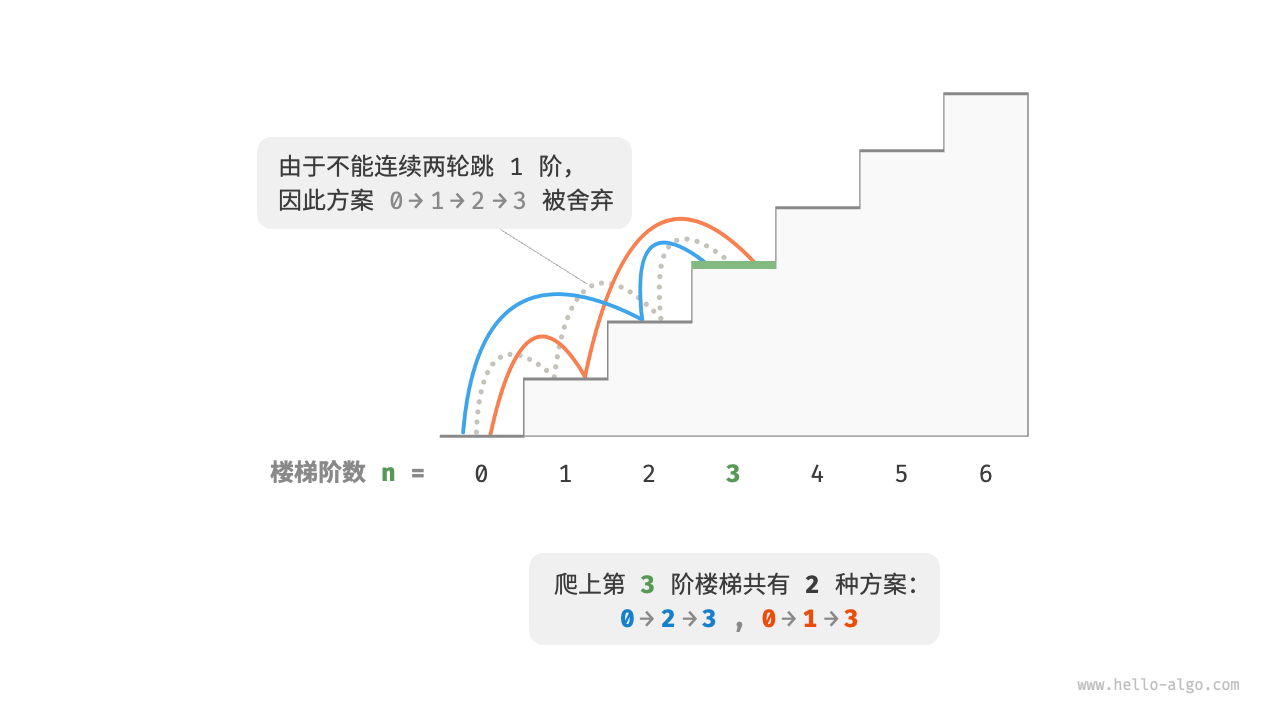
在以上问题中，如果上一轮是跳1阶而来，那么下一轮就必须是2阶。这意味着：下一步选择不能由当前状态独立决定，还和前一个状态有关。

为此，我们需要扩展状态的定义：状态[i, j]表示处在第i阶并且上一轮跳了j阶，其中j∈{1,2}。

• dp[i,1] = dp[i-1,2]：上一轮跳了1阶时，上上一轮只能选择跳2阶。
• dp[i,2] = dp[i-2,1] + dp[i-2,2]：上一轮跳2阶时，上上一轮可选择跳1阶或者2阶。
• dp[n] = dp[n,1] + dp[n,2]：两者之和代表爬到n阶的方案总数。

实现代码如下：

export default function climbingStairsConstraintDP (n) {
  if (n === 1 || n === 2) {
    return 1
  }
  // 初始化dp表，用于存储子问题的解
  const dp = Array.from(new Array(n + 1), () => new Array(3))
  // 初始状态：预设最小子问题的解
  dp[1][1] = 1
  dp[1][2] = 0
  dp[2][1] = 0
  dp[2][2] = 1
  // 状态转移：从较小子问题逐步求解较大子问题
  for(let i = 3; i <= n; i++) {
    dp[i][1] = dp[i - 1][2]
    dp[i][2] = dp[i - 2][1] + dp[i - 2][2]
  }
  return dp[n][1] + dp[n][2]
}

DP解题思路

问题判断

如果一个问题包含重叠子问题、最优子结构，并满足无后效性，那么它通常适合使用动态规划求解。然而，我们很难从问题描述中直接提取出这些特性。因此，我们通常会放宽条件，先观察问题是否适合使用回溯解决。

适合用回溯解决的问题通常满足“决策树模型”，这种问题可以使用树形结构来描述，其中每个节点代表一个决策，每条路径代表一个决策序列。

换句话说，如果问题包含明确的决策概念，并且解是通过一系列决策产生的，那么它就满足决策树模型，通常可以使用回溯来解决。

在此基础上，动态规划问题还有一些判断的加分项：

• 问题包含最大、最小、最多、最少等最优化描述。
• 问题的状态能够使用一个列表，多维矩阵或者树来表示，并且一个状态与其周围的状态存在递推关系。

相应的，也存在一些减分项：

• 问题的目标是找出所有可能得解决方案，而不是找出最优解。
• 问题描述中右明显的排列组合的特征，需要返回具体的多个方案。

问题求解步骤

动态规划的解题流程会因问题的性质和难度有所不同，但通常遵循以下步骤：描述决策、定义状态、建立dp表、推到状态转移方程、确定边界条件等。

假设有这样一个问题：给定n * m的二维网格，网格中每个单元格包含一个非负整数，表示该单元格的代价。机器人从以左上角单元格为起点，每次只能向下或者向右移动一步，直至到达右下角单元格。请返回，从左上角到右下角的最小路径和。

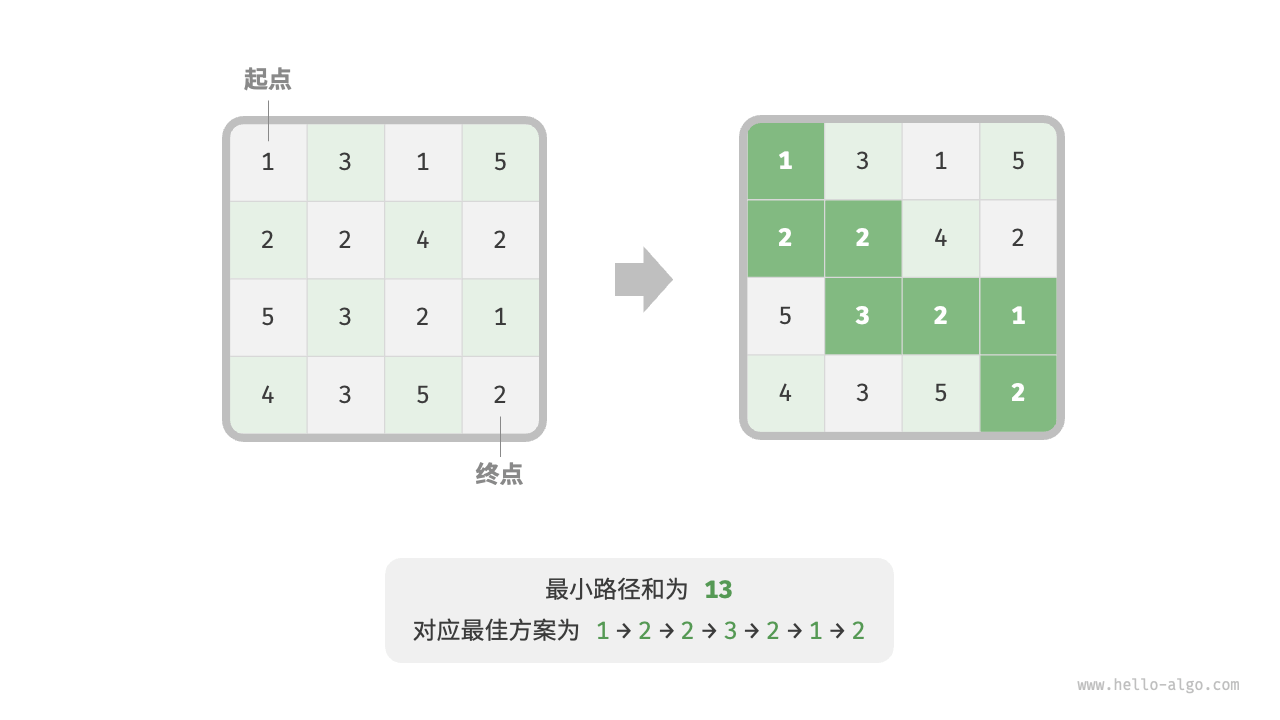
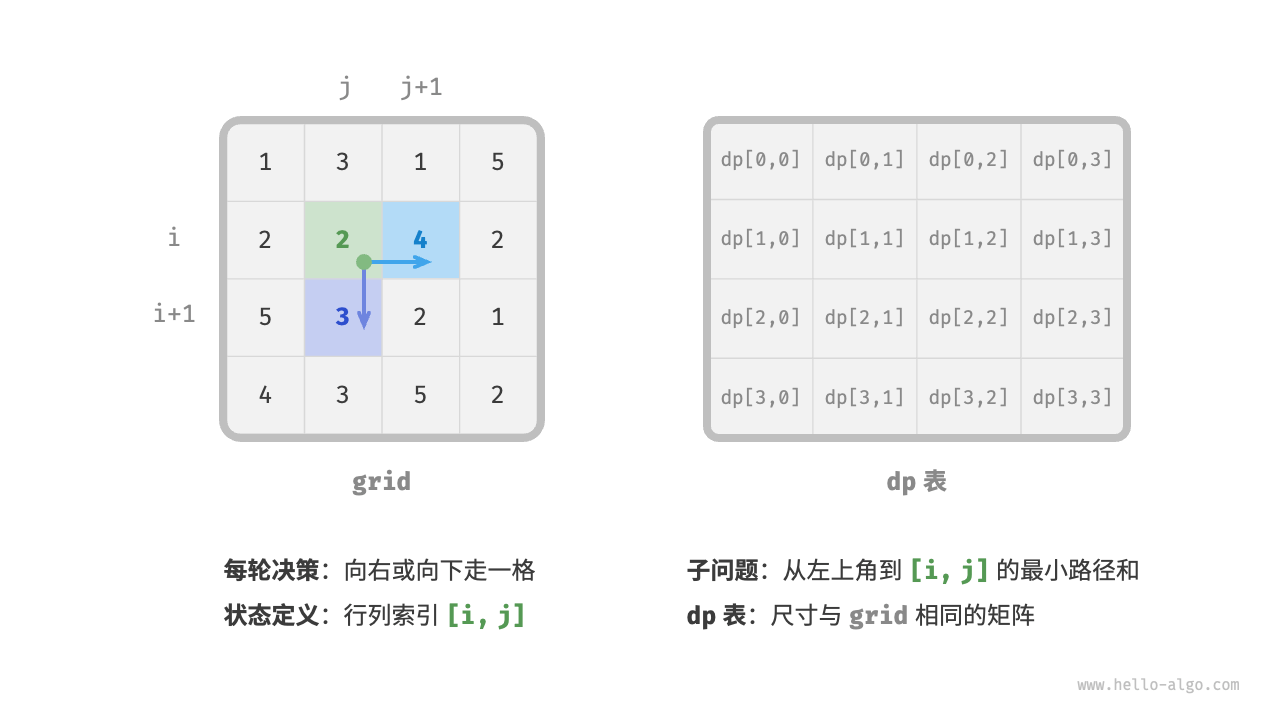
第一步：思考每轮的决策，定义状态，从而得到dp表。

• 每轮决策：从当前格子向下或者向右走一步。
• 定义状态：当前格子的行列索引为[i,j]，向下或者向右后，其对应状态分别为：[i+1,j]和[i,j+1]。
• dp表：尺寸与网格grid相同的矩阵。

第二步：找出最优子结构，进而推导出状态转移方程。

• 最优子结构：对于状态[i,j]，它只能从上边格子[i-1,j]和左边格子[i,j-1]转移而来，因此最优子结构为：到达[i,j]的最小路径和由[i-1,j]和[i,j-1]的最小路径和中较小的那一个决定。
• 状态转移方程：根据最优子结构，可以推导出其状态转移方程为：dp[i,j] = min(dp[i-1,j], dp[i,j-1]) + grid[i,j]。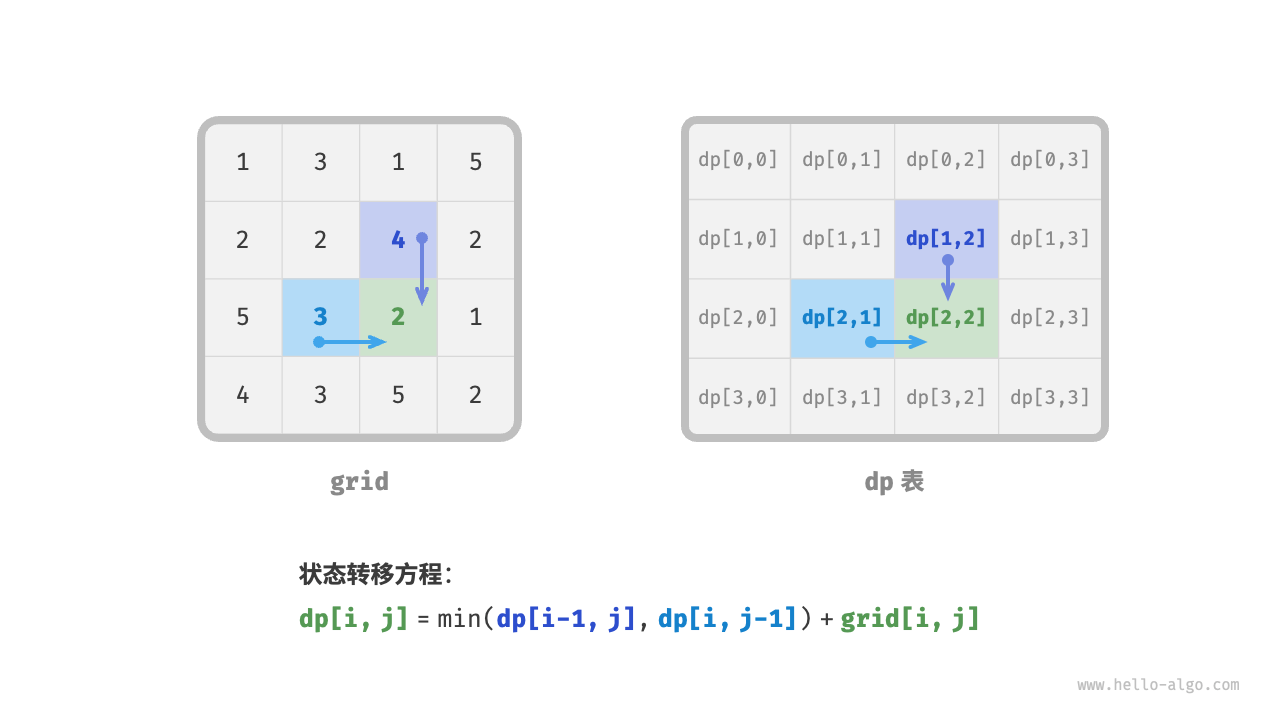

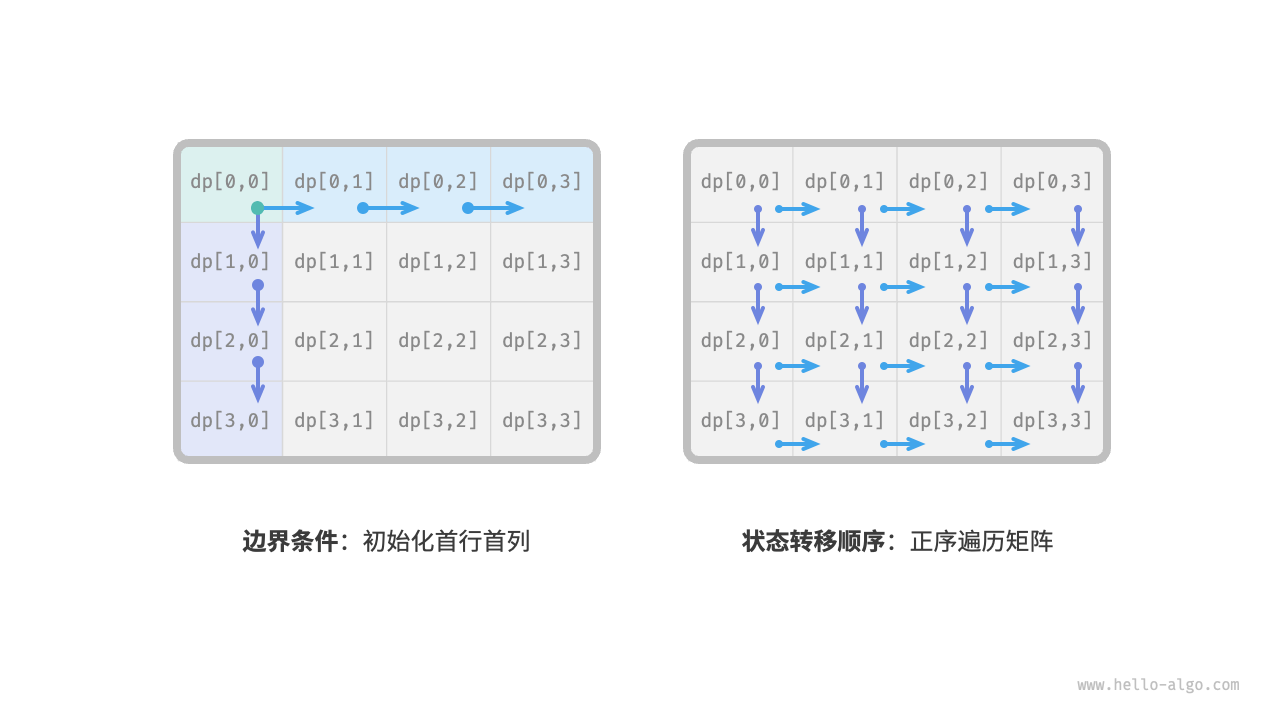
第三步：确定边界问题和状态转移顺序

• 边界问题：处在首行的状态，其只能从其左边的状态得来；处在首列的状态，其只能从其上边的状态得来。因此，首行i = 0，首列j = 0就是边界条件。
• 状态转移顺序：由于每个格子只能由其左方格子和上方格子转移而来，因此我们使用循环来遍历矩阵，外层循环遍历各行，内层循环遍历各列。

方法一：暴力搜索：

从状态[i,j]开始搜索，不断的分解为更小的状态[i-1,j]和[i,j-1]，递归函数包括以下要素：

• 递归参数：状态[i,j]
• 返回值：从[0,0]到[i,j]的最小路径和dp[i,j]
• 终止条件：当i=0且j=0时，返回代价grid[0,0]
• 剪枝：当i < 0或者j < 0时，返回代价+∞，代表不可行。

其实现代码如下：

// 方法一：暴力搜索
export const minPathSumDFS = (grid, i, j) => {
  // 终止条件
  if(i === 0 && j === 0) {
    return grid[0][0];
  }
  // 越界
  if(i < 0 || j < 0) {
    return Infinity;
  }
  // 计算左上角到[i-1,j]的最小路径和
  const left = minPathSumDFS(grid, i - 1, j);
  // 计算左上角到[i,j-1]的最小路径和
  const up = minPathSumDFS(grid, i, j - 1);
  // 计算左上角到[i,j]的最小路径和
  return Math.min(left, up) + grid[i][j];
};

暴力搜素存在一些重叠子问题，其原因是：存在多条路径可以从左上角到达某个单元格。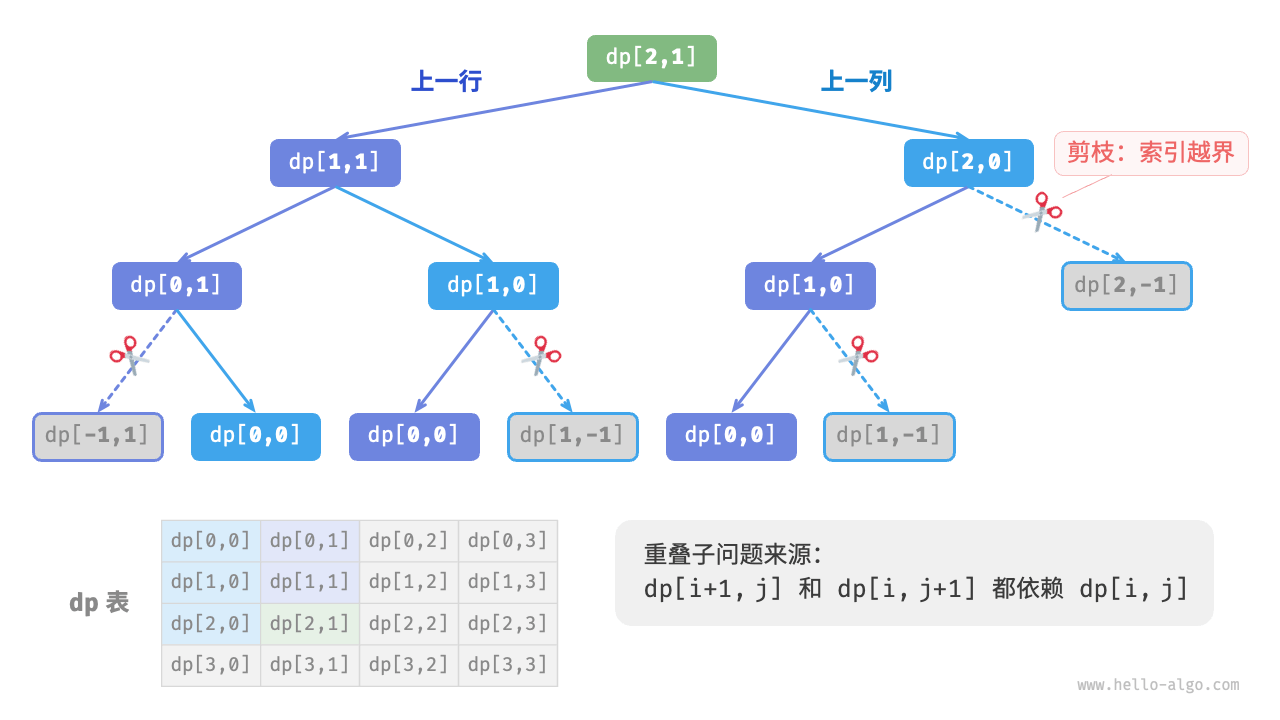

方法二：记忆化搜索：

为了解决暴力搜索中的问题，我们引入和网格grid相同大小的member记忆网格，用于记录各个问题的解，并将重叠子问题进行剪枝：

其实现代码如下：

// 方法二：记忆化搜索
export const minPathSumMemberDFS = (grid, member, i, j) => {
  // 终止条件
  if(i === 0 && j === 0) {
    return grid[0][0];
  }
  // 越界
  if(i < 0 || j < 0) {
    return Infinity;
  }
  // 剪枝：如果有记录，则直接返回
  if(member[i][j] !== -1) {
    return member[i][j];
  }
  // 计算左上角到[i-1,j]的最小路径和
  const left = minPathSumDFS(grid, i - 1, j);
  // 计算左上角到[i,j-1]的最小路径和
  const up = minPathSumDFS(grid, i, j - 1);
  // 记忆化
  member[i][j] = Math.min(left, up) + grid[i][j];
  return member[i][j];
};

在引入记忆化后，所有子问题的解只需计算一次。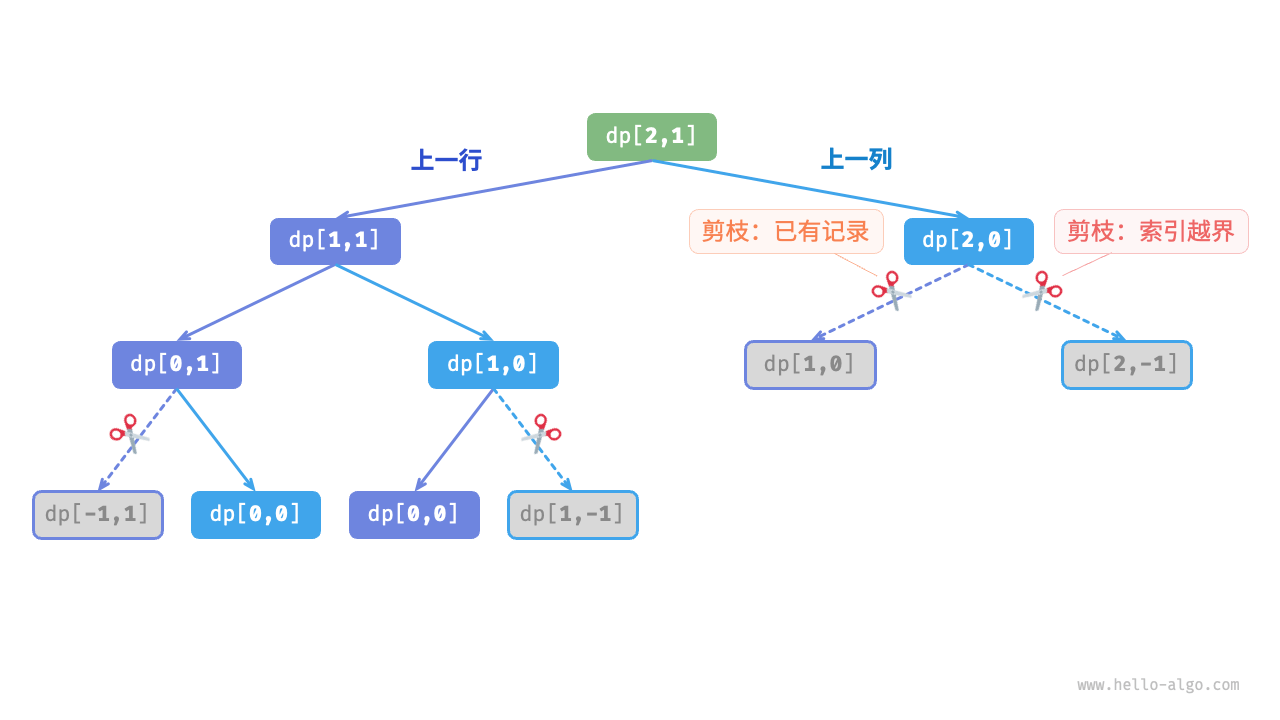

方法三：动态规划：

基于迭代实现动态规划，其代码如下：

// 方法三：动态规划
export const minPathSumDP = (grid) => {
  const n = grid.length;
  const m = grid[0].length;
  // 初始化dp表
  const dp = Array.from({ length: n }, () => Array.from({ length: m }, () => 0));
  dp[0][0] = grid[0][0];
  // 状态转移：首行
  for (let j = 1; j < m; j++) {
    dp[0][j] = dp[0][j - 1] + grid[0][j];
  }
  // 状态转移：首列
  for (let i = 1; i < n; i++) {
    dp[i][0] = dp[i - 1][0] + grid[i][0];
  }
  // 状态转移：其余行和列
  for (let i = 1; i < n; i++) {
    for (let j = 1; j < m; j++) {
      dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
    }
  }
  return dp[n - 1][m - 1];
};

空间优化：由于每个格子只与其左边和上边的格子有关，因此我们可以只用一个单行数组来实现dp表。

// 方法三：动态规划(空间优化版)
export const minPathSumDPComp = (grid) => {
  const n = grid.length;
  const m = grid[0].length;
  // 初始化dp表
  const dp = new Array(m);
  dp[0] = grid[0][0];
  // 状态转移：首行
  for (let j = 1; j < m; j++) {
    dp[j] = dp[j - 1] + grid[0][j];
  }
  // 状态转移：其余行和列
  for (let i = 1; i < n; i++){
    // 状态转移：首列
    dp[0] = dp[0] + grid[i][0];
    // 状态转移：其余列
    for (let j = 1; j < m; j++) {
      dp[j] = Math.min(dp[j], dp[j - 1]) + grid[i][j];
    }
  }
  return dp[m - 1];
};

0-1背包问题

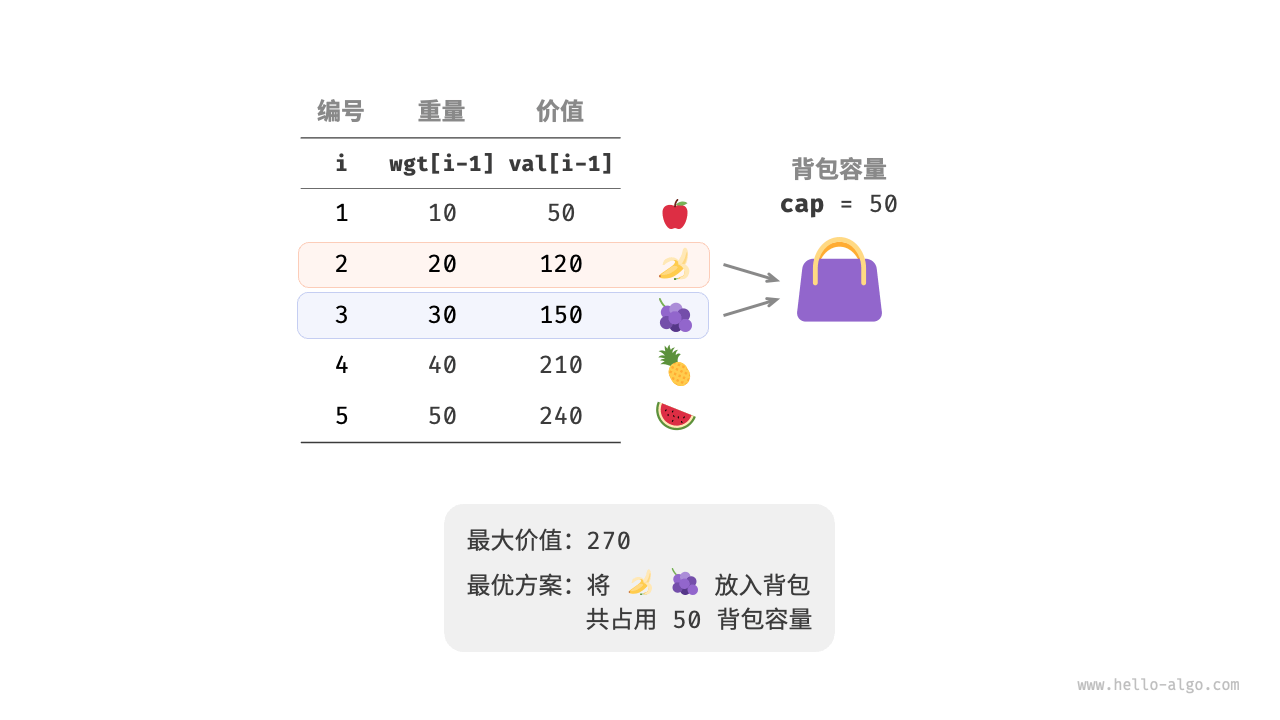
假设有这样一个问题：给定n个物品，第i个物品的重量为wgt[i - 1]、价值为val[i - 1]，和一个容量为cap的背包。每个物品只能选择一次，问在限定背包容量下能放入物品的最大价值。

第一步：思考每轮的决策、定义状态、从而得到dp表。

• 每轮决策：对于每个物品来说，可选择放入和不放入。放入时，背包容量减少，价值增加；不放入时，背包容量不变，价值不变。
• 定义状态：[i, c]，其中i表示物品编号，c表示剩余背包容量。即dp[i, c]表示第i个物品在剩余容量为c的背包中的最大价值。
• dp表：(n + 1) * (c + 1)的二维表。

第二步：找出最优子结构，进而推导出状态转移方程。 当我们做出物品i的决策后，剩余的是前i - 1个物品的决策，可分为两种情况：

1. 不放入物品i：背包容量不变，状态变化为[i - 1, c]。
2. 放入物品i：背包容量减少wgt[i - 1]，价值增加val[i - 1]，状态变化为[i - 1, c - wgt[i - 1]]。

分析完上述问题后，我们可以得出：

• 最优子结构：最大价值dp[i, c]等于不放入物品i和放入物品i两种方案种价值更大的那一个。
• 状态转移方程：dp[i, c] = max(dp[i - 1, c], dp[i - 1, c - wgt[i - 1]] + val[i - 1])。

第三步：确定边界条件和状态转移顺序。

• 边界条件：当无物品或无剩余背包容量时，最大价值为0，即首行dp[0, c]和首列dp[i, 0]都等于0。
• 状态转移顺序：当前状态[i, c]从上方状态[i - 1, c]和左上方的状态[i - 1, c - wgt[i - 1]]转移而来。

方法一：暴力搜索

暴力搜索包含以下要素：

• 递归参数：状态[i, c]。
• 返回值：子问题的解dp[i, c]
• 终止条件：当物品编号越界i = 0或背包容量为0时，终止递归并返回价值0。
• 剪枝：若当前物品重量超出背包剩余容量，则只能选择不放入。

// 方法一：暴力搜索
export const knapsackDFS = (wgt, val, i, c) => {
  // 已选完或背包容量为0，则返回价值0
  if(i === 0 || c === 0) {
    return 0;
  }
  // 物品重量超过背包剩余容量，不放入物品
  if(wgt[i - 1] > c) {
    return knapsackDFS(wgt, val, i - 1, c);
  }
  // 计算不放入物品i的最大价值
  const noVal = knapsackDFS(wgt, val, i - 1, c);
  // 计算放入物品i的最大价值
  const yesVal = knapsackDFS(wgt, val, i - 1, c - wgt[i - 1]) + val[i - 1];
  // 返回最大价值
  return Math.max(noVal, yesVal);
};

观察递归树，容易发现其中存在重复子问题，如下图：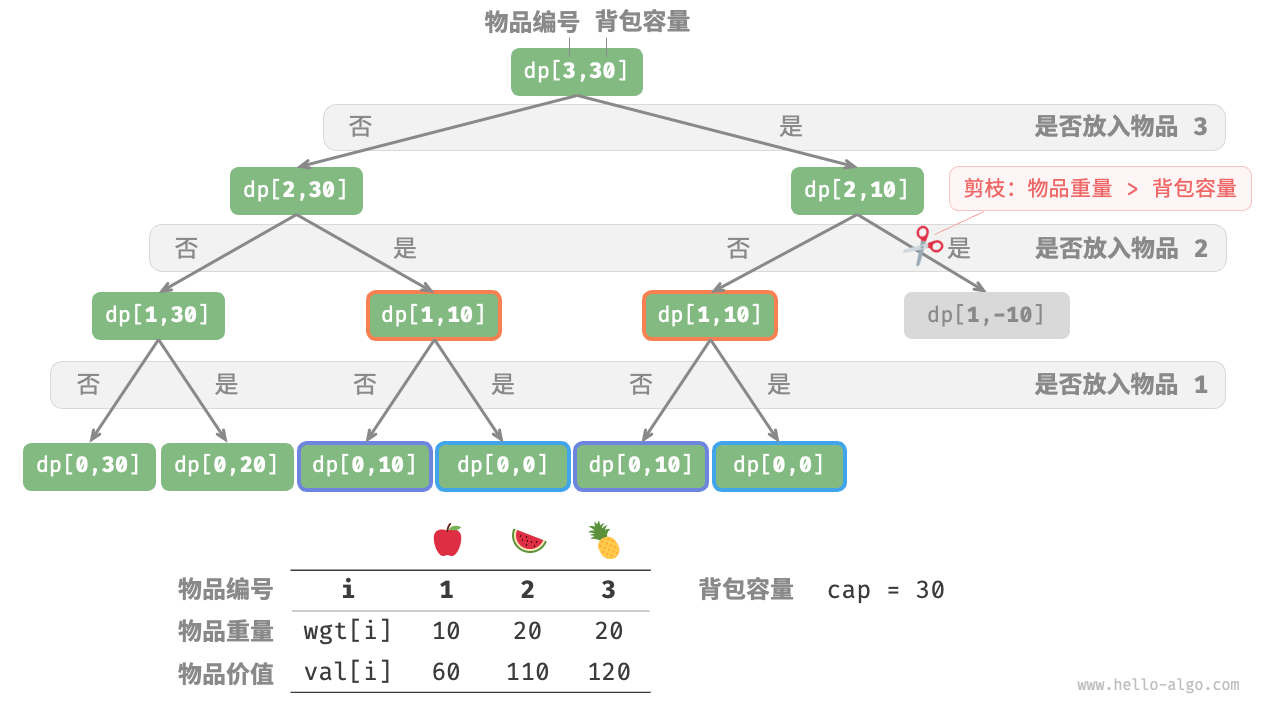

方法二：记忆化搜索

为了保证重叠子问题只被计算一次，我们可以借助记忆列表member，其中member[i][c]表示dp[i][c]。

记忆化搜索实现代码如下：

// 方法二：记忆化搜索
export const knapsackMemberDFS = (wgt, val, member, i, c) => {
  // 已选完或背包容量为0，则返回价值0
  if(i === 0 || c === 0) {
    return 0;
  }
  // 如果已被计算过，则直接返回
  if(member[i][c] !== -1) {
    return member[i][c];
  }
  // 物品重量超过背包剩余容量，不放入物品
  if(wgt[i - 1] > c) {
    return knapsackMemberDFS(wgt, val, member, i - 1, c);
  }
  // 计算不放入物品i的最大价值
  const noVal = knapsackMemberDFS(wgt, val, member,  i - 1, c);
  // 计算放入物品i的最大价值
  const yesVal = knapsackMemberDFS(wgt, val, member, i - 1, c - wgt[i - 1]) + val[i - 1];
  // 存储当前计算结果
  member[i][c] = Math.max(noVal, yesVal);
  // 返回最大价值
  return member[i][c];
};

方法三：动态规划

动态规划实质上就是在状态转移的过程中填充dp表的过程，其实现代码如下：

export const knapsackDP = (wgt, val, cap) => {
  const n = wgt.length;
  // 初始dp表
  const dp = Array.from({ length: n + 1 }, () => new Array(cap + 1).fill(0));
  // 状态转移
  for (let i = 1; i <= n; i++) {
    for (let c = 1; c <= cap; c++) {
      // 物品重量超过背包剩余容量，不放入物品
      if(wgt[i - 1] > c) {
        dp[i][c] = dp[i - 1][c];
      } else {
        dp[i][c] = Math.max(
          dp[i - 1][c],
          dp[i - 1][c - wgt[i - 1]] + val[i - 1]
        );
      }
    }
  }
  return dp[n][cap];
};

空间优化

可使用一个一维数组，其中内层循环倒序遍历，如下：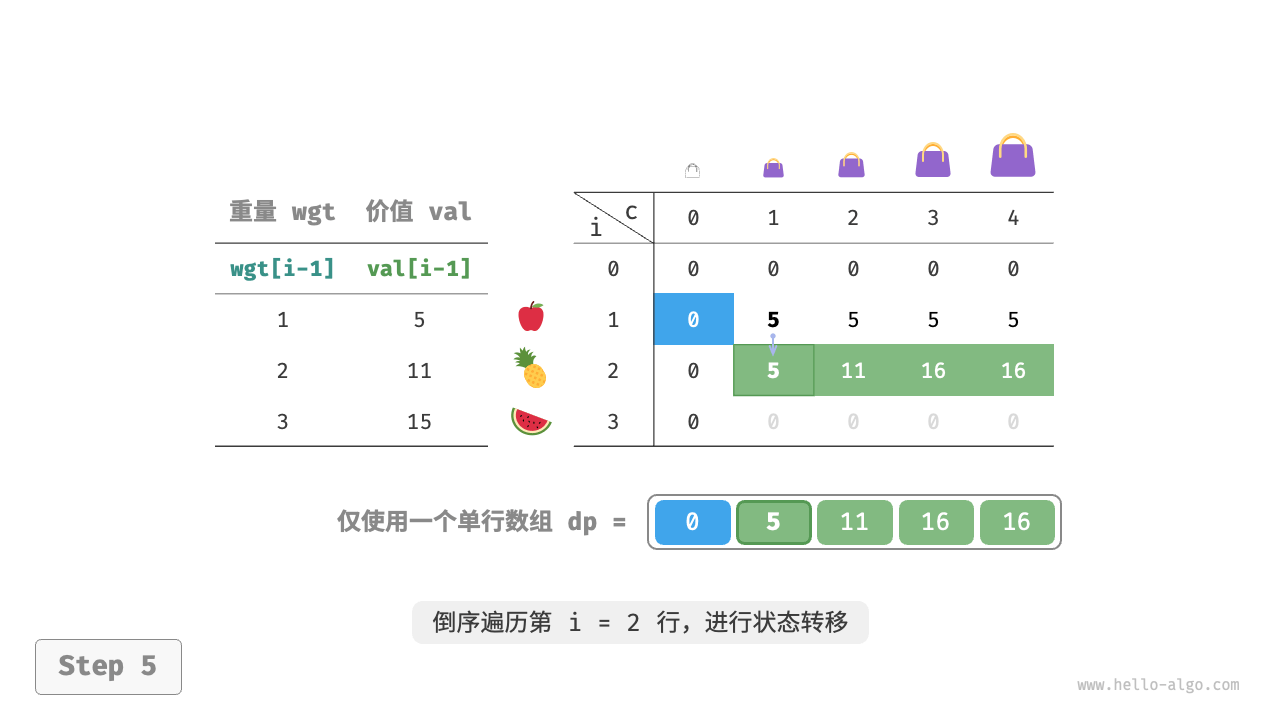

其空间优化代码如下：

export const knapsackDPComp = (wgt, val, cap) => {
  const n = wgt.length;
  // 初始dp表
  const dp = new Array(cap + 1).fill(0);
  // 状态转移
  for (let i = 1; i <= n; i++) {
    for(let c = cap; c >= 1; c--) {
      if(wgt[i - 1] <= c) {
        dp[c] = Math.max(
          dp[c],
          dp[c - wgt[i - 1]] + val[i - 1]
        );
      }
    }
  }
  return dp[cap];
};

完全背包问题

完全背包问题和0-1背包问题非常相似，它们的区别仅在于不限制物品的选择次数。

完全背包问题

假设给定n个物品，第i个物品的重量为wgt[i-1]、价值为val[i-1]和一个容量为cap的背包。每个物品可以重复选取，问在限定背包容量下能放下物品的最大价值。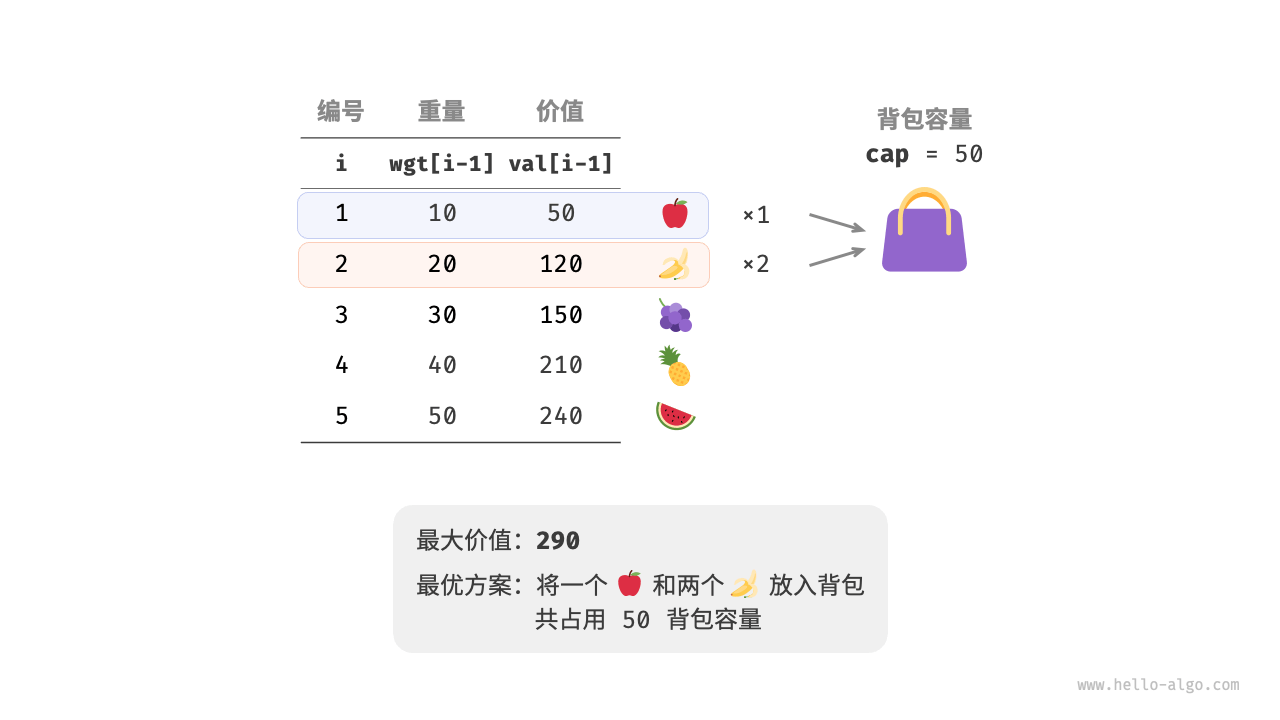

动态规划思路

• 在0-1背包问题中，每种物品只有一个，因此将物品i放入背包后，只能从前i-1个物品中选择。
• 在完全背包问题中，每种物品的数量是无限的，因此将物品i放入背包后，任然可以从前i个物品中选择。

在完全背包问题的规定下，状态[i, c]的变化分两种情况。

• 不放入物品i，与0-1背包问题相同，转移至[i-1, c]。
• 放入物品i，与0-1背包问题不同，转移至[i, c-wgt[i-1]]。

因此，状态转移方程为：dp[i, c] = max(dp[i-1, c] + dp[i, c-wgt[i-1]] + val[i-1])

代码实现

export const unboundedKnapsackDP = (wgt, val, cap) => {
  const n = wgt.length;
  // 初始dp表
  const dp = Array.from({ length: n + 1 }, () => new Array(cap + 1).fill(0));
  // 状态转移
  for (let i = 1; i <= n; i++) {
    for (let c = 1; c <= cap; c++) {
      // 物品重量超过背包剩余容量，不放入
      if(wgt[i - 1] > c) {
        dp[i][c] = dp[i - 1][c];
      } else {
        // 
        dp[i][c] = Math.max(
          dp[i - 1][c],
          dp[i][c - wgt[i - 1]] + val[i - 1]
        );
      }
    }
  }
  return dp[n][cap];
};

空间优化

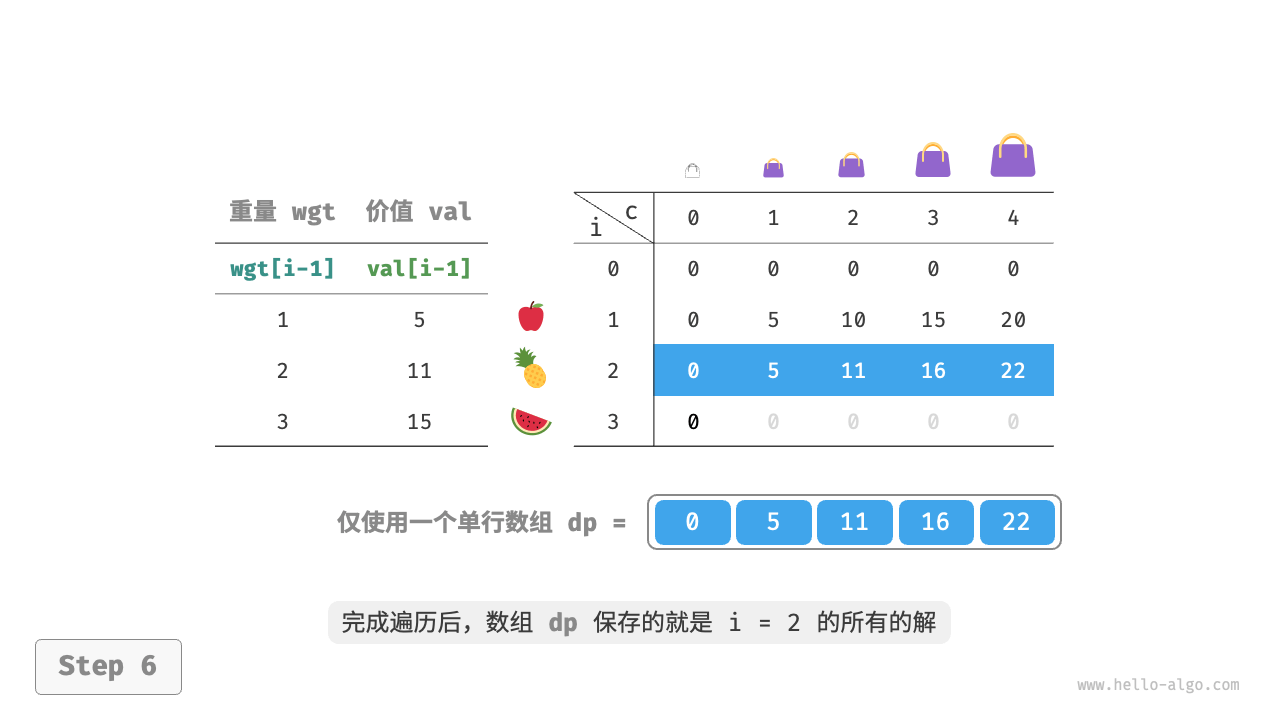
由于当前状态是由左边和上边的状态转移而来，因此空间优化后应该对dp表中的每一行进行正序遍历，这个0-1背包问题正好相反。

export const unboundedKnapsackComp = (wgt, val, cap) => {
  const n = wgt.length;
  // 初始dp表
  const dp = new Array(cap + 1).fill(0);
  // 状态转移
  for (let i = 1; i <= n; i++) {
    for(let c = 1; c <= cap; c++) {
      if(wgt[i - 1] <= c) {
        dp[c] = Math.max(
          dp[c],
          dp[c - wgt[i - 1]] + val[i - 1]
        );
      }
    }
  }
  return dp[cap];
};

零钱兑换问题Ⅰ

给定n种硬币，第i种硬币的面值为coins[i - 1]，目标金额为amt，每种硬币可以重复选取，问能够凑出目标金额的最少硬币数量。如果无法凑出，则返回-1。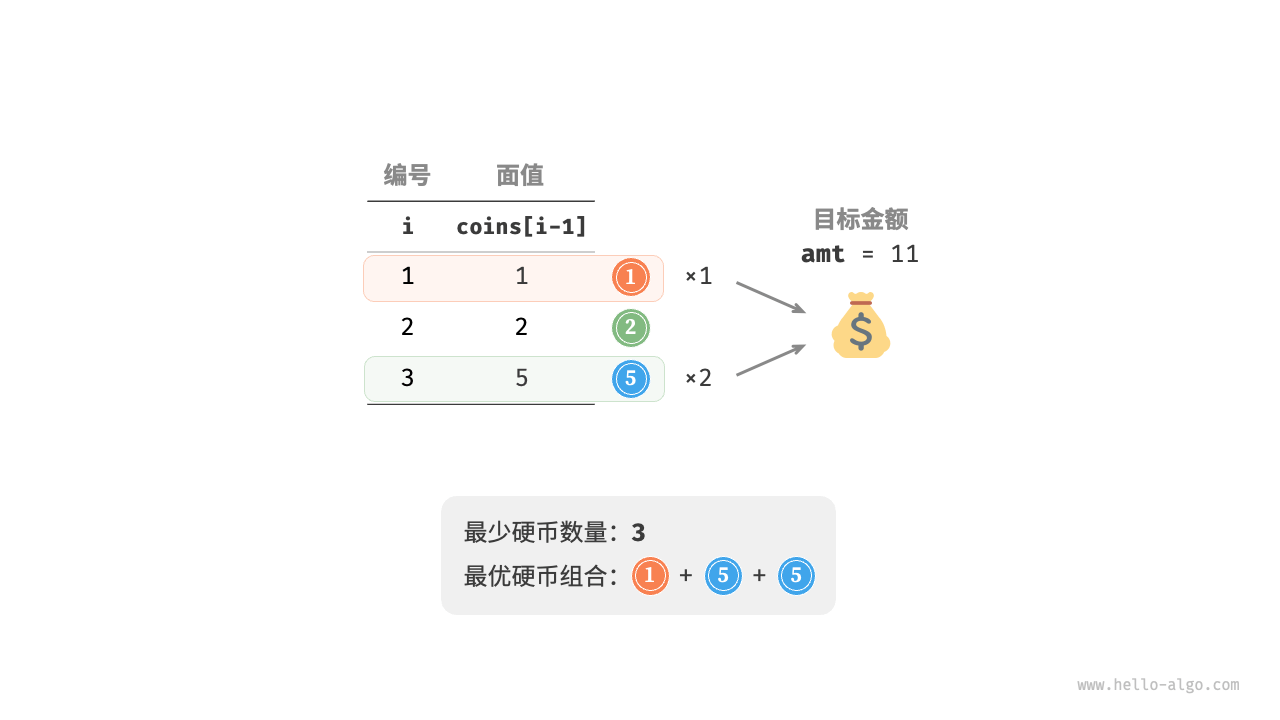

动态规划思路

零钱兑换可以看做是完全背包问题的一种特殊情况，两者具有以下联系和不同点。

• 两道题可以相互转换：物品对应硬币，物品重量对应硬币面值，背包容量对应目标金额。
• 优化目标相反：完全背包问题是最大化物品价值，零钱兑换问题是最小化硬币数量。
• 求解目的不同：完全背包问题是求不超过背包最大容量下的解，零钱兑换问题求恰好凑到目标金额的解。

第一步：思考每轮决策，定义状态，进而得出dp表。 状态[i, a]对应的子问题为：前i种硬币能够凑出金额a的最小硬币数量，记为dp[i, a]。二维dp表为(n + 1) * (amt + 1)。

第二步：找出最优子结构，进而推导出状态转移方程。 本问题和完全背包问题的状态转移方程存在以下差异：

• 本题求解最小值，所有需要使用min代替完全背包问题中的max。
• 优化主体是硬币数量而非商品价值，因此在选中硬币时执行+1即可。 根据以上分析，状态转移方程定义为：dp[i, a] = min(dp[i - 1, a], dp[i, a - coins[i - 1]] + 1)

第三步：确定边界条件和状态转移顺序。 当目标金额为0时，凑出它的最少硬币数量为0，即首列dp[i, 0]都为0。当无硬币时，无法凑出任意 > 0的目标金额，即无效解。

代码实现

使用amt + 1代表无效解，其代码实现如下：

export const coinChangeDP = (coins, amt) => {
  const n = coins.length;
  const max = amt + 1;
  // 初始化dp表
  const dp = Array.from({ length: n + 1 }, () => Array.from({ length: max }, () => 0));
  // 首行、首列
  for (let a = 1; a <= amt; a++) {
    dp[0][a] = max;
  }
  // 状态转移：其余行和列
  for (let i = 1; i <= n; i++) {
    for (let a = 1; a <= amt; a++) {
      if(coins[i - 1] > a) {
        // 目标金额超出，不选择
        dp[i][a] = dp[i - 1][a];
      } else {
        // 不选择和选硬币i这两种方案的较小值
        dp[i][a] = Math.min(
          dp[i - 1][a],
          dp[i][a - coins[i - 1]] + 1
        );
      }
    }
  }
  return dp[n][amt] !== max ? dp[n][amt] : -1;
};

空间优化

零钱兑换问题的空间优化和完全背包问题一致：

export const coinChangeDPComp = (coins, amt) => {
  const n = coins.length;
  const max = amt + 1;
  // 初始化dp表
  const dp = Array.from({ length: max }, () => max);
  dp[0] = 0;
  // 状态转移
  for (let i = 1; i <= n; i++) {
    for (let a = 1; a <= amt; a++) {
      if(coins[i - 1] <= a) {
        dp[a] = Math.min(
          dp[a],
          dp[a - coins[i - 1]] + 1
        );
      }
    }
  }
  return dp[amt] !== max ? dp[amt] : -1;
};

零钱兑换问题Ⅱ

给定n种硬币，第i中硬币的面值为coins[i - 1]，目标金额为amt，每种硬币可以重复选取，问能够凑出目标金额的硬币组合数量。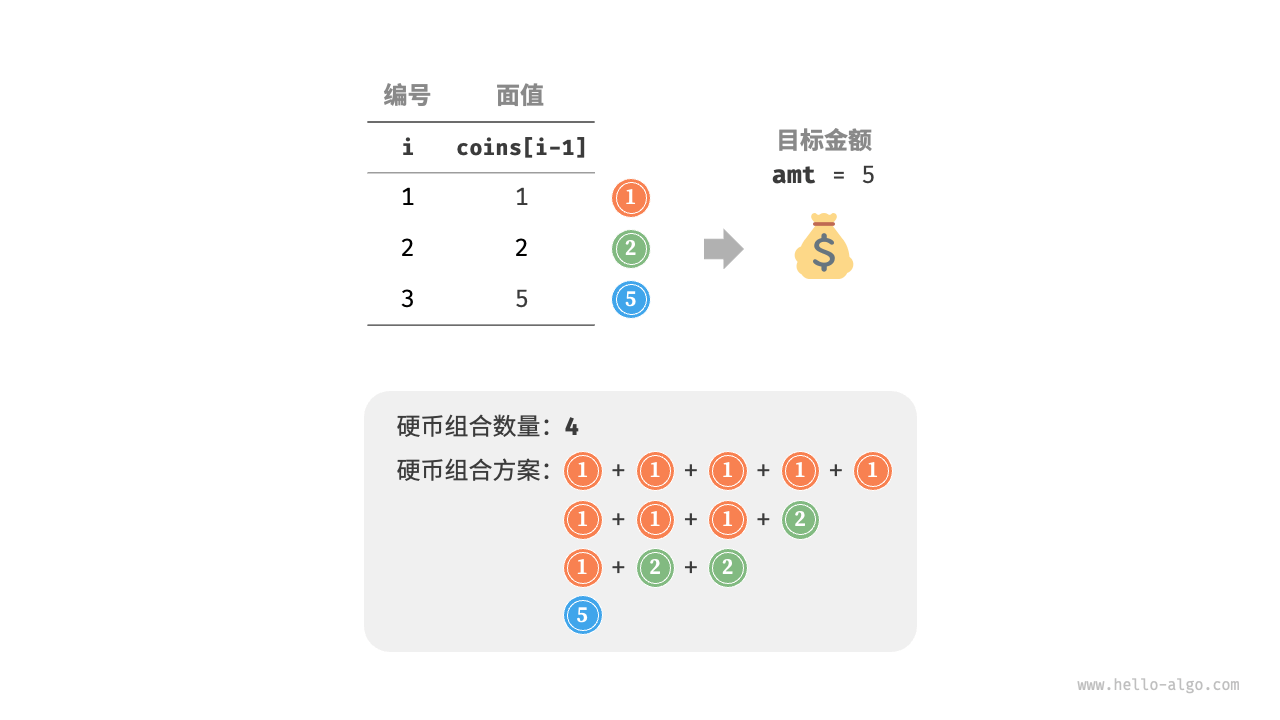

动态规划思路

相较于上一题，本题的目标是求组合数量，因此子问题变为：前i中硬币能够凑出金额为a的组合数量，而dp二维表的尺寸依旧。

状态转移方程为：dp[i, a] = dp[i - 1, a] + dp[i - 1, a - coins[i - 1]]。

当目标金额为0时，无须选择任何硬币即可凑出目标金额，因此应将首列dp[i, 0]赋值为1；当无隐蔽时，无法凑出符合条件的金额，即dp[0, a]赋值为0。

代码实现

export const coinChangeIIDP = (coins, amt) => {
  const n = coins.length;
  // 初始dp表
  const dp = Array.from({ length: n + 1 }, () => Array.from({ length: amt + 1 }, () => 0));
  // 首列
  for (let i = 0; i <= n; i++) {
    dp[i][0] = 1;
  }
  // 状态转移
  for (let i = 1; i <= n; i++) {
    for (let a = 1; a <= amt; a++) {
      if(coins[i - 1] > a) {
        // 超出目标金额，不选
        dp[i][a] = dp[i - 1][a];
      } else {
        // 不选和选择i，这两种方案之和
        dp[i][a] = dp[i - 1][a] + dp[i][a - coins[i - 1]];
      }
    }
  }
  return dp[n][amt];
};

空间优化

export const coinChangeIIDPComp = (coins, amt) => {
  const n = coins.length;
  // 初始dp表
  const dp = Array.from({ length: amt + 1 }, () => 0);
  dp[0] = 1;
  // 状态转移
  for (let i = 1; i <= n; i++) {
    for (let a = 1; a <= amt; a++) {
      if(coins[i - 1] <= a) {
        // 不选和选择i，这两种方案之和
        dp[a] = dp[a] + dp[a - coins[i - 1]];
      }
    }
  }
  return dp[amt];
};

编辑距离问题

编辑距离问题：是指狂歌字符串之间互相转换的最小次数，通常用于在信息检索和自然语言处理中度量两个序列的相似度。

假设输入两个字符串s和t，返回将s转换为t的最小编辑步数。你可以在字符串中进行三种编辑操作：插入一个字符，删除一个字符和替换一个字符。编辑距离问题可以很自然的用决策树模型来解释，字符串对应树节点，一轮决策对应树的一条边。

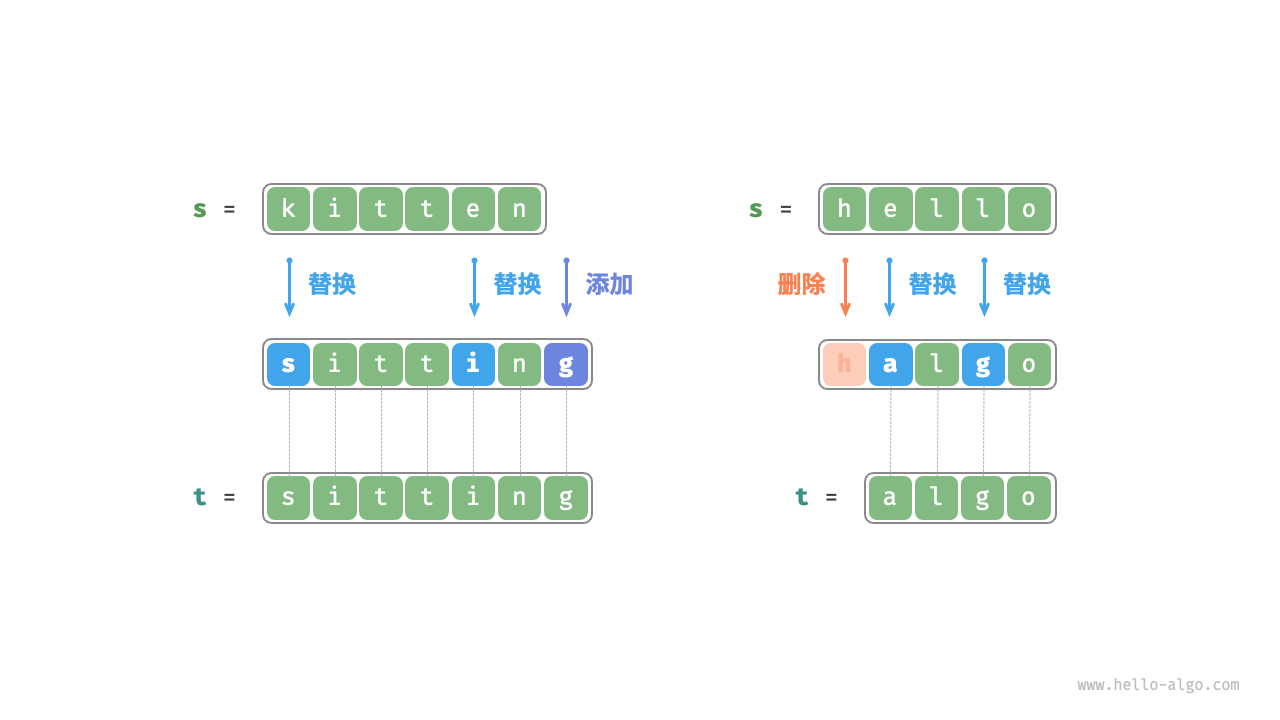
动态规划思路

第一步：思考每轮的决策，定义状态，进而得到dp表：

每一轮的决策是对字符串s进行一次编辑操作，我们希望在编辑操作的过程中，问题的规模逐渐缩小，这样才能构建子问题。

设字符串s和t的长度分别为n和m，我们先考虑两字符串尾部的字符s[n - 1]和t[m - 1]。

• 若s[n - 1]和t[m - 1]相同，则可以跳过它们，直接考虑s[n - 2]和t[m - 2]。
• 若s[n - 1]和t[m - 1]不相同，我们需要对s进行一次编辑操作(插入，删除或者替换)，使得两字符的尾部字符相同。

因此，将状态定义为字符串s和t中，分别对应的第i和第j个字符，记为[i, j]。状态[i, j]对应的子问题即为：将字符串s的前i个字符更改为t的前j个字符所需的最小编辑步数。

至此，得到一个尺寸为(i + 1) * (j + 1)的二维dp表。

第二步：找出最优子结构，进而推导出状态转移方程：

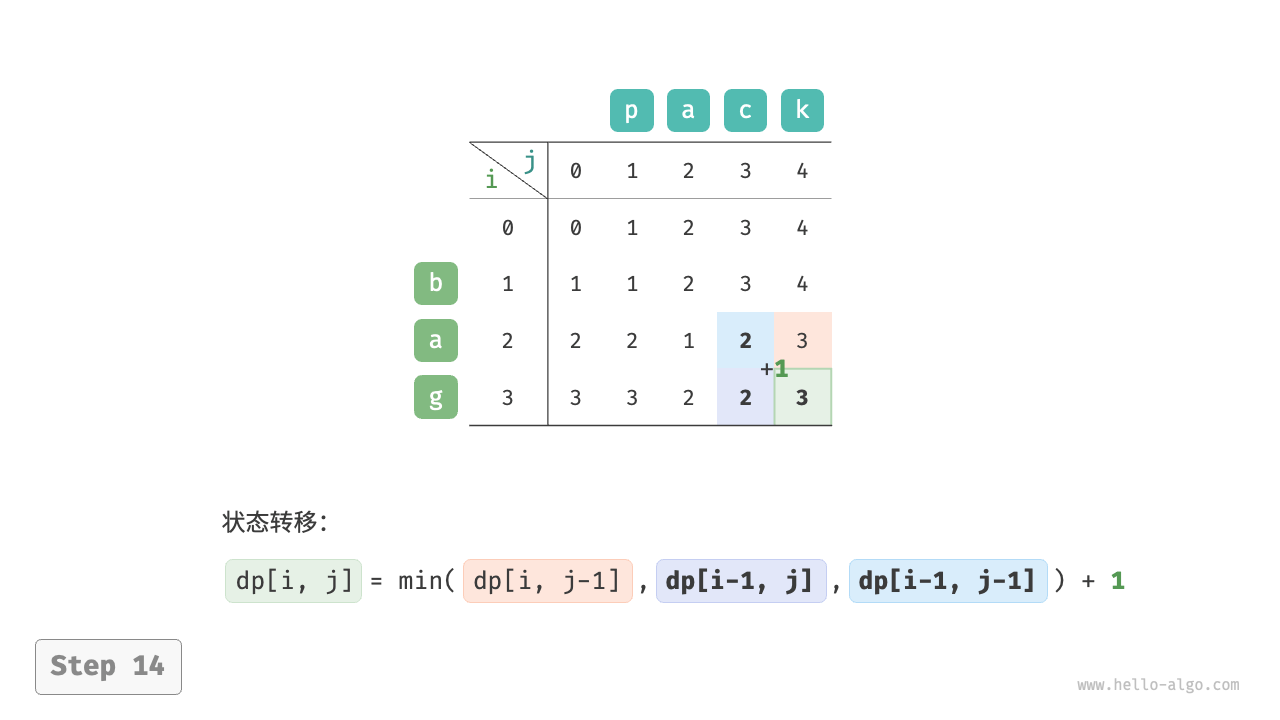
考虑子问题dp[i, j]，其对应的两个字符串的尾部字符为s[i - 1]和t[j - 1]，可根据不同的编辑分三种情况：

• 在s[i - 1]之后添加t[j - 1]，则剩余子问题为dp[i, j - 1]。
• 删除s[i - 1]，则剩余子问题为dp[i - 1, j]。
• 将s[i - 1]替换为t[j - 1]，则剩余子问题dp[i - 1, j - 1]。

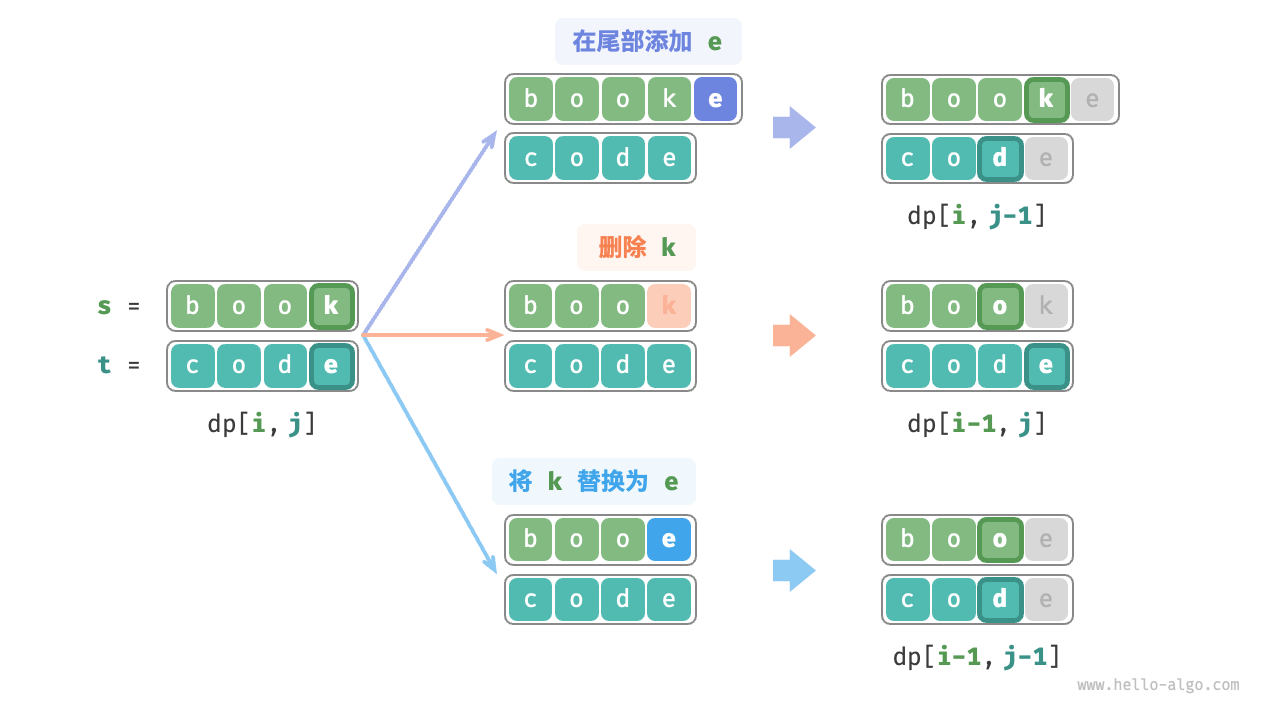
根据以上分析，其状态转移方程为：dp[i, 1] = min(dp[i, j - 1], dp[i - 1, j], dp[i - 1, j - 1]) + 1

第三步：确定边界条件和状态转移顺序：

• 当两个字符串为空时，编辑步数为0，即dp[0, 0] = 0。
• 当s为空但t不为空时，最小编辑距离等于t的长度，即首行dp[0, j] = j。
• 当s不为空但t为空时，最小编辑距离等于s的长度，即首列dp[i, 0] = i。

代码实现

// 最少编辑距离问题：DP
export const editDistanceDP = (s, t) => {
  const n = s.length;
  const m = t.length;
  const dp = Array.from({ length: n + 1 }, () => new Array(m + 1).fill(0));

  // 状态转移：首行，首列
  for (let i = 1; i <= n; i++) {
    dp[i][0] = i;
  }
  for (let j = 1; j <= m; j++) {
    dp[0][j] = j;
  }

  // 状态转移：其余行和列
  for (let i = 1; i <= n; i++) {
    for (let j = 1; j <= m; j++) {
      if (s.charAt(i - 1) === t.charAt(j - 1)) {
        // 字符相等，直接跳过
        dp[i][j] = dp[i - 1][j - 1];
      } else {
        // 最小编辑步数：插入、删除、替换这三种操作的最小编辑步数 + 1
        dp[i][j] = Math.min(
          dp[i][j - 1],
          dp[i - 1][j],
          dp[i - 1][j - 1]
        ) + 1;
      }
    }
  }

  return dp[n][m];
};

空间优化

由于dp[i, j]是由上方dp[i - 1, j]，左方dp[i, j - 1]和左上方dp[i - 1, j - 1]转移而来，而正序遍历会丢失左上方dp[i - 1, j - 1]，倒序遍历无法提前构建dp[i, j - 1]，因此两种遍历顺序都不可取。

为此，我们使用一个变量leftUp来暂时存放左上方的解，从而只考虑左方和上方的解。

// 最小编辑距离问题：空间优化
export const editDistanceDPComp = (s, t) => {
  const n = s.length;
  const m = t.length;
  const dp = new Array(m + 1).fill(0);

  // 状态转移：首行
  for (let j = 1; j <= m; j++) {
    dp[j] = j;
  }
  // 状态转移：其余行
  for (let i = 1; i <= n; i++) {
    let leftUp = dp[0];
    dp[0] = i;
    for (let j = 1; j <= m; j++) {
      const temp = dp[j];
      if (s.charAt(i - 1) === t.charAt(j - 1)) {
        dp[j] = leftUp;
      } else {
        dp[j] = Math.min(dp[j - 1], dp[j], leftUp) + 1;
      }
      
      leftUp = temp;
    }
  }

  return dp[m];
};

参考

• Hello 算法 动态规划