图
图:是一种非线性数据结构,由顶点(vertex)和边(edge)组成。可以将图G抽象的表示为一组顶点V和一组边E的集合。
相较于线性关系(链表)和分治关系(树),网络关系(图)的自由度更高,因而更为复杂。 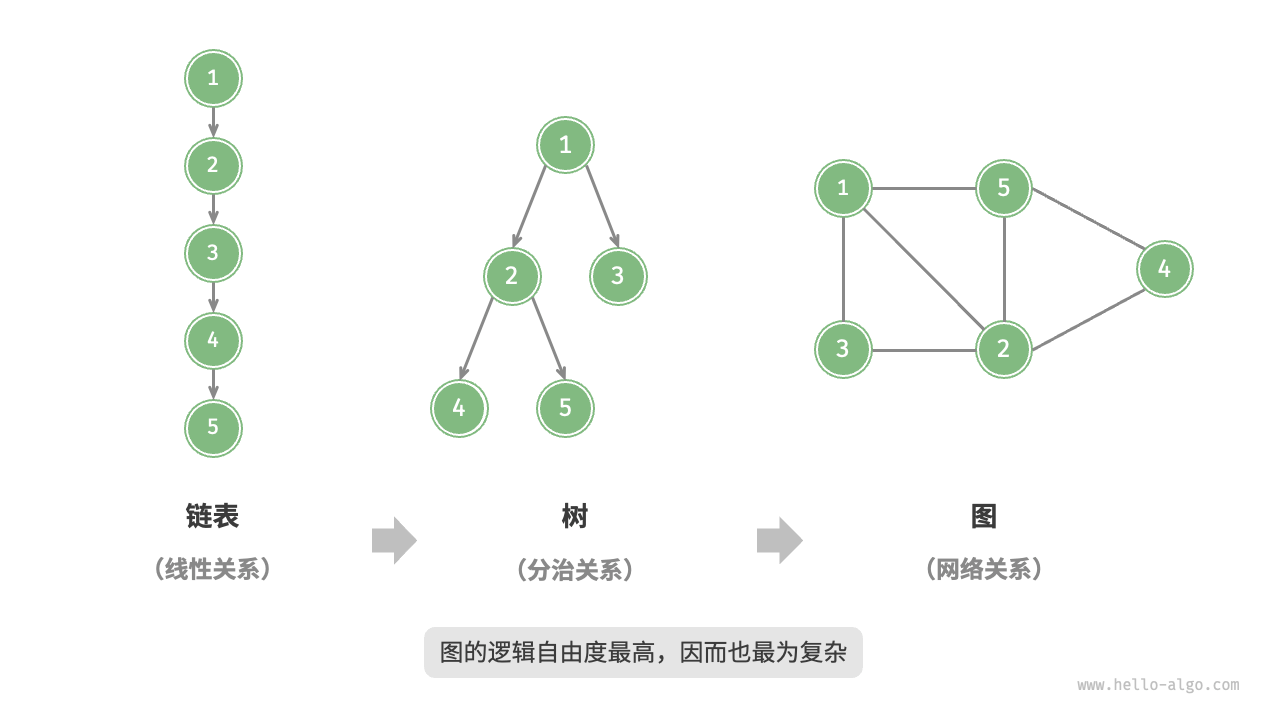
在图中,其常见术语如下:
- 邻接adjacency: 当两个顶点有边相连时,称这两个顶点邻接。
- 路径path:从顶点A到顶点B所经过的边构成的序列,称A到B的路径。
- 度degree:一个顶点拥有的边数。在有向图中,入度表示有多少条边指向该节点。出度表示有多少条边从这个顶点指出。
图
图的常见类型
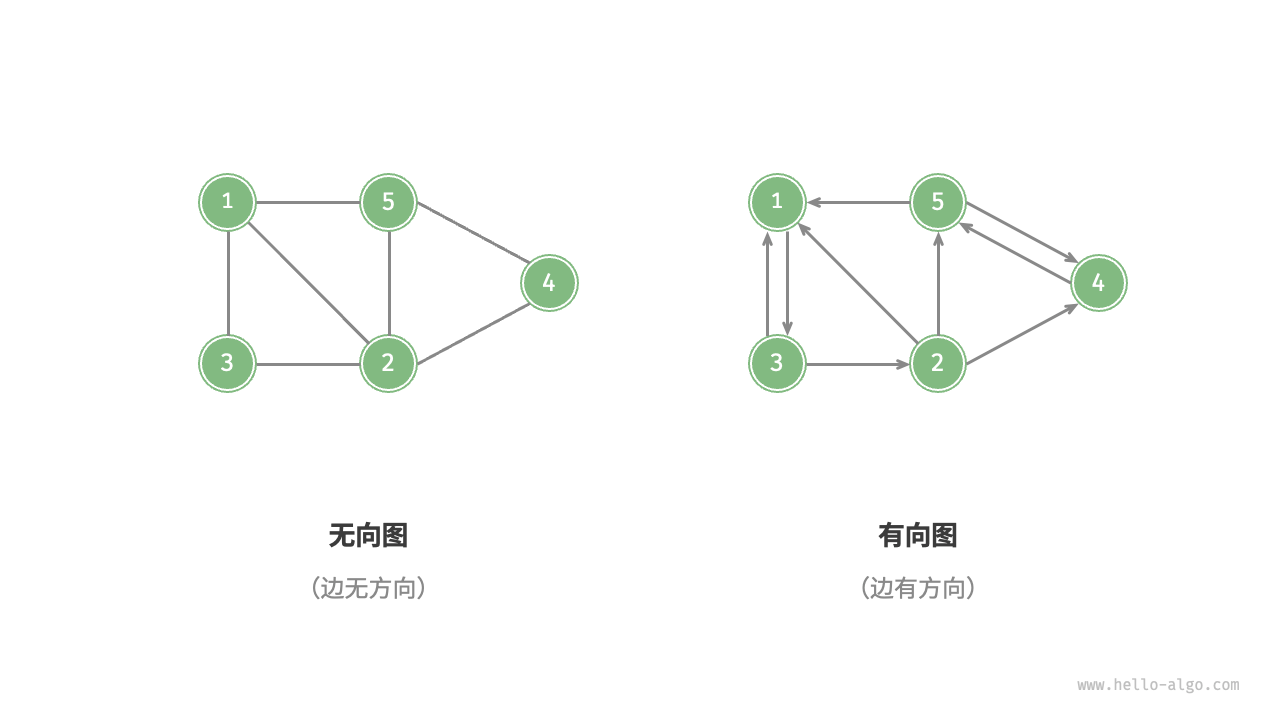
根据边是否有方向,可以将图划分为:
- 有向图:在有向图中,边具有方向,即A => B和 B => A两个方向是相互独立的,例如社交网络中的关注和被关注的关系。
- 无向图:在无向图中,边表示两顶点之间的双向连接关系,例如社交网络中的好友关系。
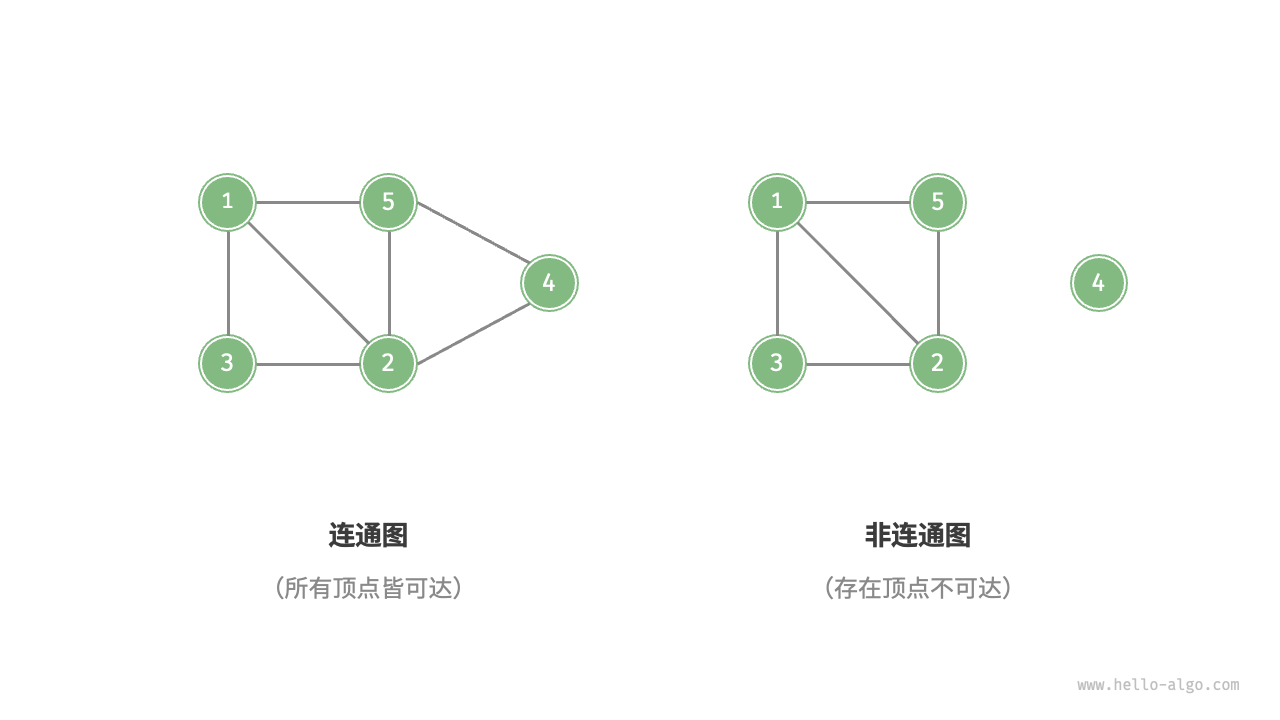
根据所有顶点是否连通,可以将图划分为:
- 非连通图:在非连通图中,从某个顶点触发,至少有一个顶点是无法到达的。
- 连通图:在连通图中,从某个顶点触发,可以到达其它任意顶点。
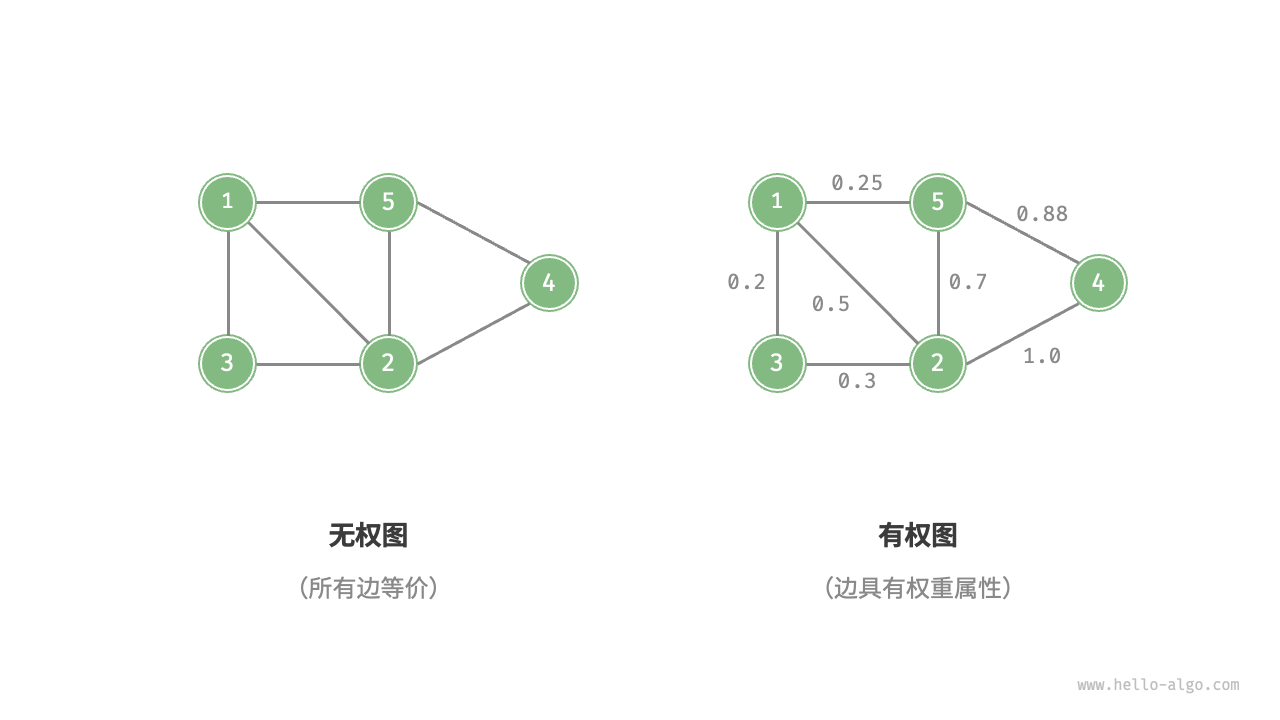
根据边是否添加权重,可以将图划分为:
- 无权图:即普通图。
- 有权图:在有权图中,会为每条边添加一个数值,依据数值关系,可以达到某种程序目的。例如亲密度网络。
图的表示
图的表示方式通常有:邻接矩阵和邻接表两种方式。
邻接矩阵:设顶点数量为N,邻接矩阵adjacency matrix使用N * N大小的矩阵来表示图,每一行、每一列代表一个顶点,矩阵元素代表边。在矩阵中,使用0和1表示两个顶点之间是否存在边。
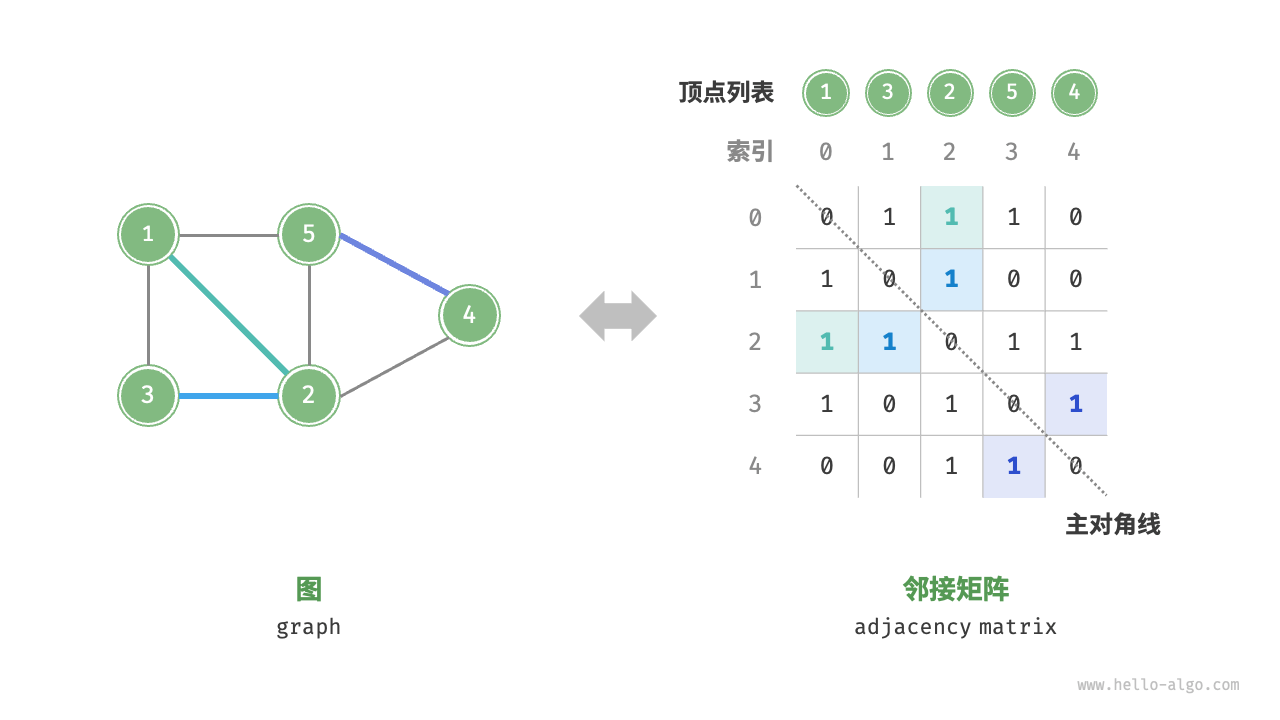
邻接矩阵有如下特点:
- 顶点不能和自身相连,因此矩阵的主对角线元素没有意义。
- 对于无向图,两个方向的边是等价的,因此邻接矩阵关于主对角线对称。
- 将邻接矩阵的元素,从
0/1换成权重,则可表示有权图。 - 可以直接访问矩阵元素以获取边,因此邻接矩阵的增、删、查、改的效率非常高,时间复杂度都是
O(1),然而矩阵空间的复杂度为O(n),需要占用更多的内存。
邻接表:使用后N个链表来表示图,其中链表头结点表示顶点,其它链表节点表示与头结点相邻的其它顶点。
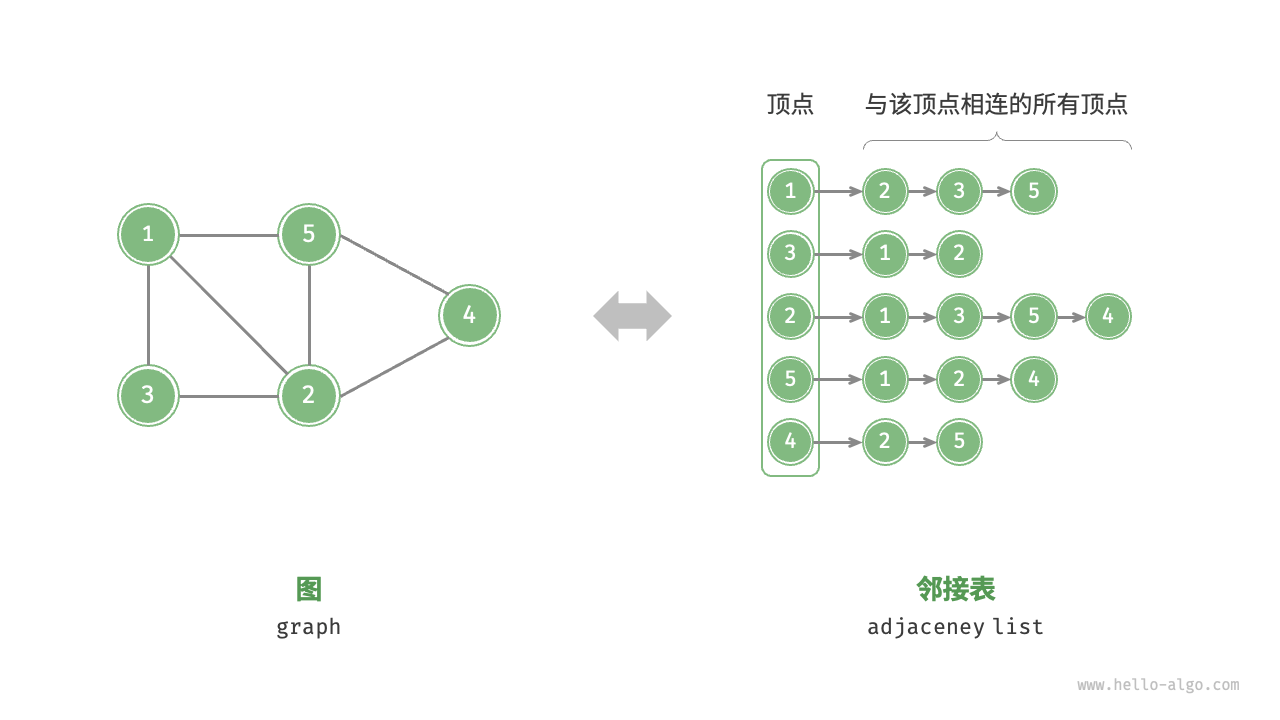
邻接表有如下特点:
- 仅存储实际存在的边,而边的总数通常远小于N²,所以更节省内存。然而需要遍历链表查找表,时间效率不如邻接矩阵。
- 可以把邻接表转化为
AVL树或红黑树,将时间效率优化到O(logn)。或者转换为哈希表,将时间效率优化到O(1)。
图的基本操作和实现
图的基本操作可分为对边的操作和对顶点的操作两种。
基于邻接矩阵的实现
假设给定一个顶点数量为N的无向图,其相关操作如下:
init(): 初始化图。addEdge(i, i): 添加边。removeEdge(i, j): 删除边。addVertex(val): 添加顶点。removeVertex(index): 删除顶点。getSize():获取顶点数量。getVertices():获取顶点列表getAdjacencyMatrix():获取邻接矩阵。
完整实现,请参考基于邻接矩阵实现的图
基于邻接表的实现
假设无向图的顶点总数为N,边数为M,其相关操作如下:
init(): 初始化图。addEdge(v1, v2): 添加边。removeEdge(v1, v2): 删除边。addVertex(v): 添加顶点。removeVertex(v): 删除顶点。getSize(): 获取顶点数量。getAdjacencyList():获取邻接表。
完整实现,请参考基于邻接表实现的图
效率对比
假设图中有N个顶点和M条边,则以上两种实现方案的效率对比如下:
| 操作 | 邻接矩阵 | 邻接表(链表) | 邻接表(哈希表) |
|---|---|---|---|
| 判断是否邻接 | O(1) | O(m) | O(1) |
| 添加边 | O(1) | O(1) | O(1) |
| 删除边 | O(1) | O(m) | O(1) |
| 添加顶点 | O(n) | O(1) | O(1) |
| 删除顶点 | O(n²) | O(n + m) | O(n) |
| 内存占用 | O(n²) | O(n + m) | O(n + m) |
整体来看,基于邻接矩阵实现的图,体现了以空间换时间的思想;而基于邻接表实现的图,则体现了以时间换空间的思想。
图的遍历
广度优先遍历(BFS)
广度优先遍历是一种由近及远的遍历方式,从某个节点出发,始终优先访问距离最近的顶点,并一层层向外扩张。
在图中,会以左上角顶点出发,首先遍历该顶点的邻接顶点,然后再下一个顶点的所有邻接顶点,以此类推,直至遍历完毕。 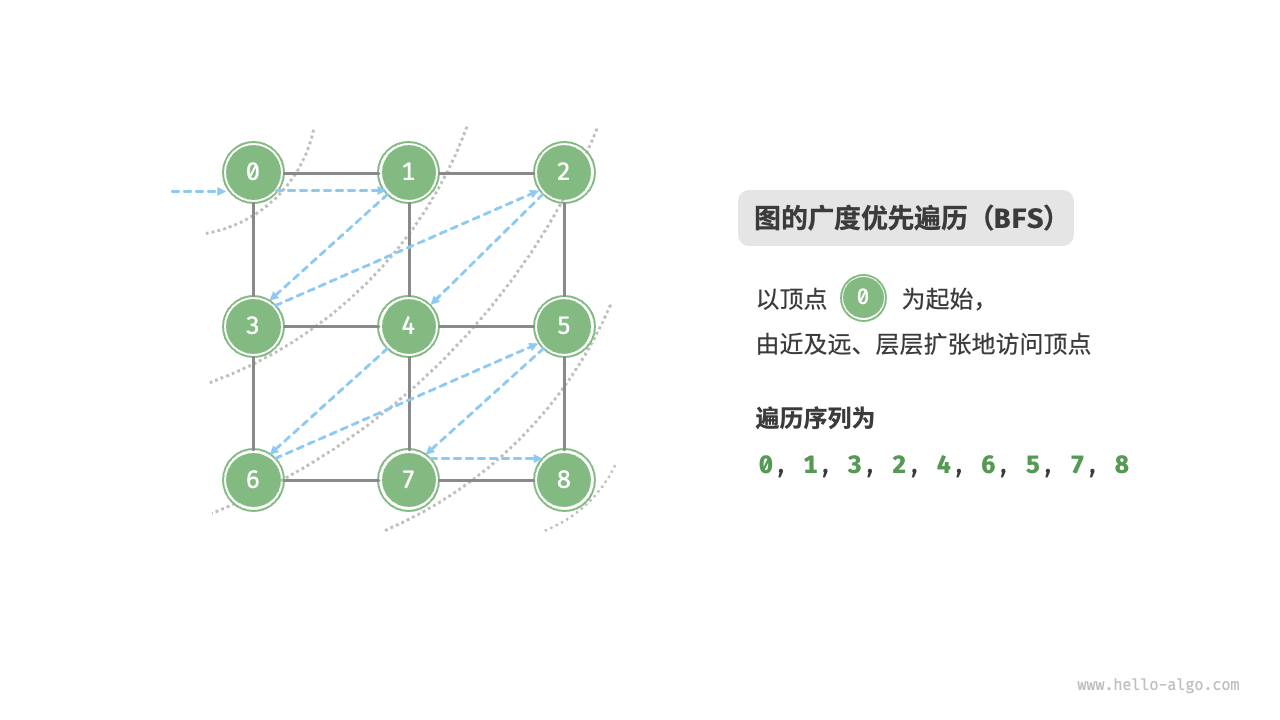
图的广度优先遍历实现思路如下:
- 将遍历起始顶点加入队列中。
- 在循环的每轮中,弹出队首元素并记录访问节点,然后将该顶点的所有邻接顶点加入队尾。
- 循环步骤二,直至所有顶点被遍历完毕。
假设有N个顶点和M条边,其复杂度如下:
- 时间复杂度:
O(n + m), 所有顶点会完成一次入队和出队的操作,每条边会被访问两次。 - 空间复杂度:
O(n),已访问顶点列表和队列都会占用内存空间,O(n + n)。
基于邻接表实现的BFS完整代码,请参考基于邻接表实现图的广度优先遍历
深度优先遍历(DFS)
深度优先遍历是一种优先走到底、无路可走再回头的遍历方式。
在图中,会以左上角顶点出发,访问当前顶点的某个邻接顶点,直到走到尽头时返回,再继续走到尽头时返回,以此类推,直至遍历完毕。
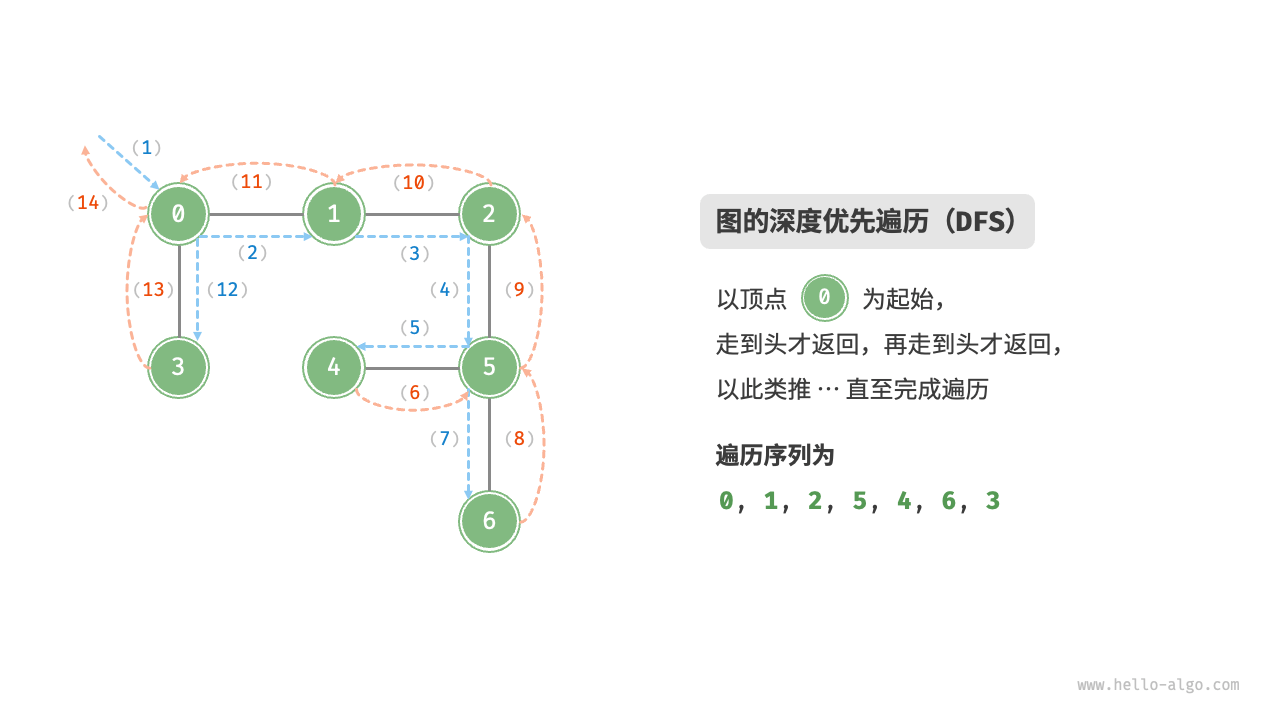
假设有N个顶点和M条边,其复杂度如下:
- 时间复杂度:
O(n + m), 所有顶点会被访问一次,每条边会被访问两次。 - 空间复杂度:
O(n),哈希表内存开销和递归调用栈内存开销,O(n + n)。
基于邻接表实现的DFS完整代码,请参考基于邻接表实现图的深度优先遍历