哈希表

基本概念

HashTable哈希表，又称散列表，其通过建立key和value之间的映射关系，实现高效的元素查询。

例如：我们规定有N个学生，每个学生都有学号和姓名两项数据，我们希望实现输入学号，返回学生姓名的查询功能，则可以采用如下哈希表来实现。学生哈希表

除哈希表以外，通常还会用链表和数组实现查询功能，三者效率对比如下：

操作	数组	链表	哈希表
查找元素	O(n)	O(n)	O(1)
添加元素	O(1)	O(1)	O(1)
删除元素	O(n)	O(n)	O(1)

通过以上表可见：在哈希表中进行增、删、查、改操作时间复杂度都是O(1)，非常高效。

哈希表的常见操作有：初始化、添加键值对和删除键值对。其遍历方式一般有：键值对遍历、键遍历和值遍历。

// 初始化
const map = new Map();

// 添加键值对
map.set(12836, '小哈');
map.set(15937, '小啰');
map.set(16750, '小算');
map.set(13276, '小法');
map.set(10583, '小鸭');

// 查询操作
const name = map.get(15937)
console.log(name) // 小罗

// 删除键值对
map.delete(10583)

// 键值对遍历
for(let [k, v] of map.entries()) {
  console.log(k, v)
}

// 键遍历
for(let k of map.keys()) {
  console.log(k)
}

// 值遍历
for(let v of map.values()) {
  console.log(v)
}

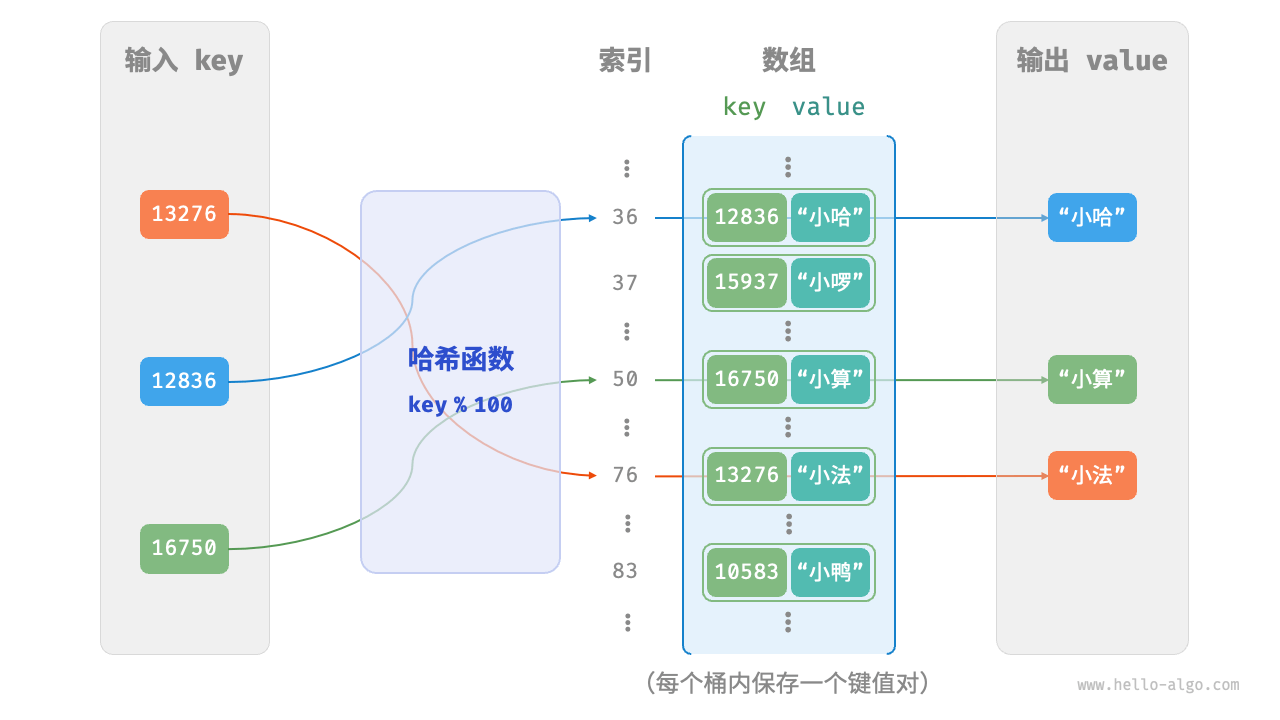
基于上面通过学号查询学习姓名的功能，考虑最简单的情况，可以使用数组来实现一个哈希表。

输入：学生学号。
过程：通过学生学号，得到其所在数组中的索引位置。这个过程由哈希函数来实现。
输出：学生姓名。

完整代码，请参考数组实现哈希表open in new window

哈希实现案例

哈希冲突

function hashFunc (key) {
  return key % 100;
}

从以上哈希函数的实现中，很容易可以看出问题：当key超过100时，存在两个不同的key对应同一个索引位置的问题，例如：

110 % 100 === 10 % 100

针对以上情况，我们称之为哈希冲突。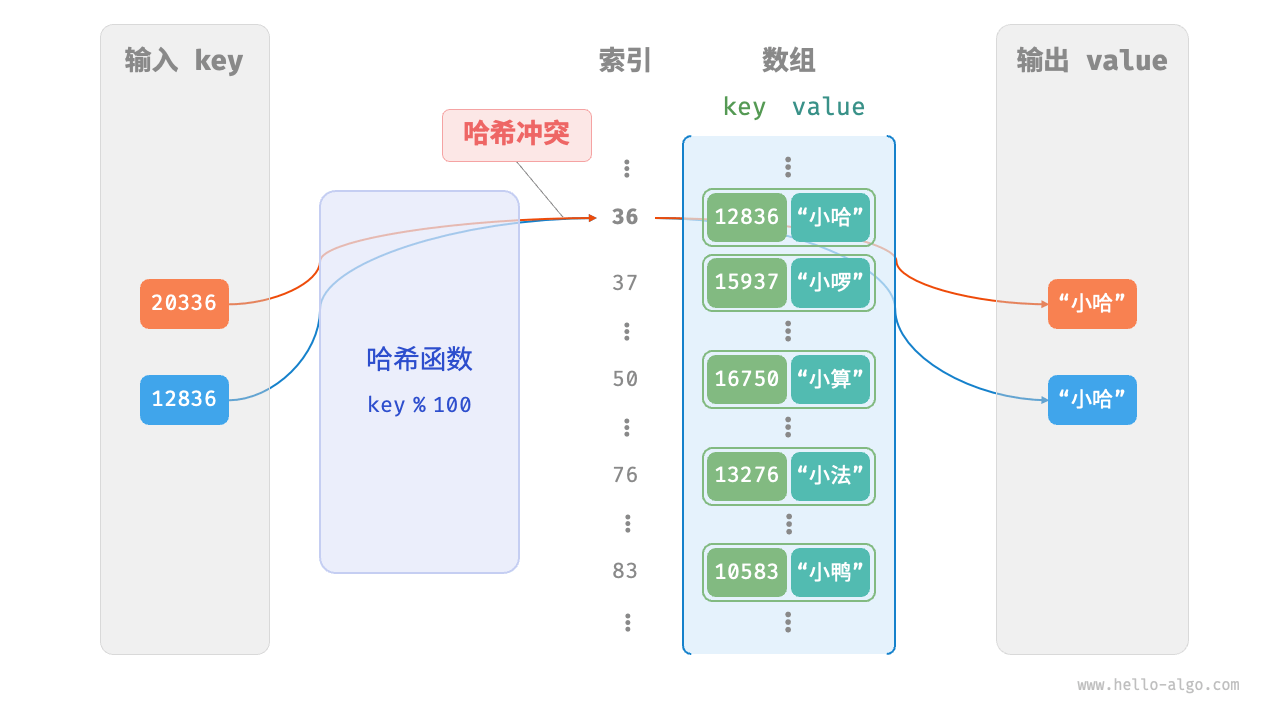

再次审视哈希函数的实现和哈希冲突问题，很容易想到一种解决办法：哈希表容量N越大，多个key被分配到同一个空间的概率就越低，冲突就越少，我们称之为哈希表扩容。

类似于数组的扩容，哈希表扩容需要将原来的键值对重新计算，并重新分配到新的哈希表中，这个过程非常耗时。

基于哈希表扩容机制，衍生出一个重要概念：负载因子，其定义为：哈希表元素的数量除以哈希表的容量，用负载因子来衡量哈希表冲突的严重程度，也常被用于哈希表扩容的触发条件。

在Java语言中，当负载因子超过0.75时，系统会将哈希表的容量扩展到原来的两倍。

哈希冲突解决办法

当哈希发生冲突时，直接扩容简单粗暴且有效，但其效率实在太低。其它常见的解决办法有：

链式地址：将哈希表中值只能存储单一元素，调整为链表，当此key发生哈希冲突时，值当做链表节点进行存储。
开放寻址：不引入额外的数据结构，当哈希发生冲突时，通过多次探测来处理哈希冲突，探测的方式主要有：线性探测、平方探测以及多次哈希等。

链式地址

在原始哈希表中，每个桶只能存储一个键值对，链式地址将单个元素转换为链表结构，将键值对作为链表节点，将所有发生冲突的键值对存储在同一个链表中。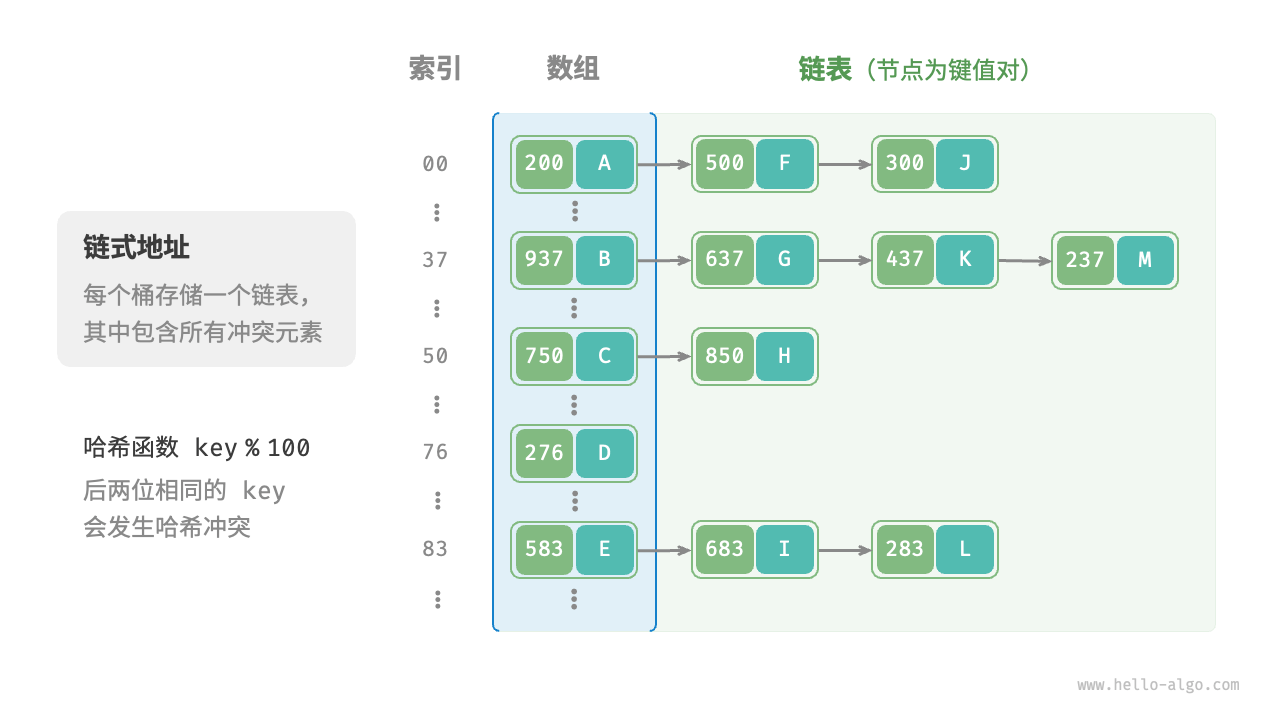哈希表链式地址法

链式地址办法其特点如下：

查询元素：输入key，根据哈希函数得到链表头结点，然后遍历链表并对比key以查询到目标键值对链表节点。
添加元素：输入key，根据哈希函数得到链表头结点，然后遍历链表至尾部，添加键值对链表节点。
删除元素：输入key，根据哈希函数得到链表头结点，然后遍历链表并对比key以删除目标键值对链表节点
内存开销：需要额外存储链表指针，比数组实现方式内存开销更大。
查询效率：链表为线性存储，相比数组实现查询效率会降低。

链表实现方式，请参考链表实现哈希表open in new window

哈希算法

无论是链式地址还是开发寻址，其只能保证在发生哈希冲突时可以正常工作，但无法减少哈希冲突的发生。

既然哈希冲突时由哈希函数所决定，我们的重点应该放在哈希函数的设计上。

哈希算法的目标

对于哈希函数，其一般目标如下：

确定性：对于相同的输入，哈希算法应始终产生相同的输出。这样才能确保哈希表是可靠的。
效率高：计算哈希值的过程应该足够快。计算开销越小，哈希表的实用性越高。
均匀分布：哈希算法应使得键值对平均分布在哈希表中。分布越平均，哈希冲突的概率就越低。

对于密码学中的应用，要求哈希函数有如下目标：

单向性：无法通过哈希值反推出关于输入数据的任何信息。
抗碰撞性：应当极其困难找到两个不同的输入，使得它们的哈希值相同。
雪崩效应：输入的微小变化应当导致输出的显著且不可预测的变化。

哈希算法的设计

TIP

当使用大质数作为模数时，可以最大化地保证哈希值的均匀分布。

哈希算法的设计是一个需要考虑许多因素的复杂问题。然而对于某些要求不高的场景，我们也能设计一些简单的哈希算法

加法哈希：对输入的每个字符的 ASCII 码进行相加，将得到的总和作为哈希值。
乘法哈希：利用了乘法的不相关性，每轮乘以一个常数，将各个字符的 ASCII 码累积到哈希值中。
异或哈希：将输入数据的每个元素通过异或操作累积到一个哈希值中。
旋转哈希：将每个字符的 ASCII 码累积到一个哈希值中，每次累积之前都会对哈希值进行旋转操作。

/* 加法哈希 */
function addHash(key) {
  let hash = 0;
  const MODULUS = 1000000007;
  for (const c of key) {
    hash = (hash + c.charCodeAt(0)) % MODULUS;
  }
  return hash;
}

/* 乘法哈希 */
function mulHash(key) {
  let hash = 0;
  const MODULUS = 1000000007;
  for (const c of key) {
    hash = (31 * hash + c.charCodeAt(0)) % MODULUS;
  }
  return hash;
}

/* 异或哈希 */
function xorHash(key) {
  let hash = 0;
  const MODULUS = 1000000007;
  for (const c of key) {
    hash ^= c.charCodeAt(0);
  }
  return hash & MODULUS;
}

/* 旋转哈希 */
function rotHash(key) {
  let hash = 0;
  const MODULUS = 1000000007;
  for (const c of key) {
    hash = ((hash << 4) ^ (hash >> 28) ^ c.charCodeAt(0)) % MODULUS;
  }
  return hash;
}

常见的哈希算法

在实际中，我们通常会用一些标准哈希算法，例如 MD5、SHA-1、SHA-2、SHA3 等。它们可以将任意长度的输入数据映射到恒定长度的哈希值。近一个世纪以来，哈希算法处在不断升级与优化的过程中。一部分研究人员努力提升哈希算法的性能，另一部分研究人员和黑客则致力于寻找哈希算法的安全性问题。

	MD5	SHA-1	SHA-2	SHA-3
推出时间	1992	1995	2002	2008
输出长度	128 bits	160 bits	256 / 512 bits	224/256/384/512 bits
哈希冲突	较多	较多	很少	很少
安全等级	低，已被成功攻击	低，已被成功攻击	高	高
应用	已被弃用，仍用于数据完整性检查	已被弃用	加密货币交易验证、数字签名等	可用于替代 SHA-2

参考

Hello 算法哈希表open in new window

# 哈希表

# 基本概念

# 哈希冲突

# 哈希冲突解决办法

# 链式地址

# 哈希算法

# 哈希算法的目标

# 哈希算法的设计

# 常见的哈希算法

# 参考

哈希表