堆

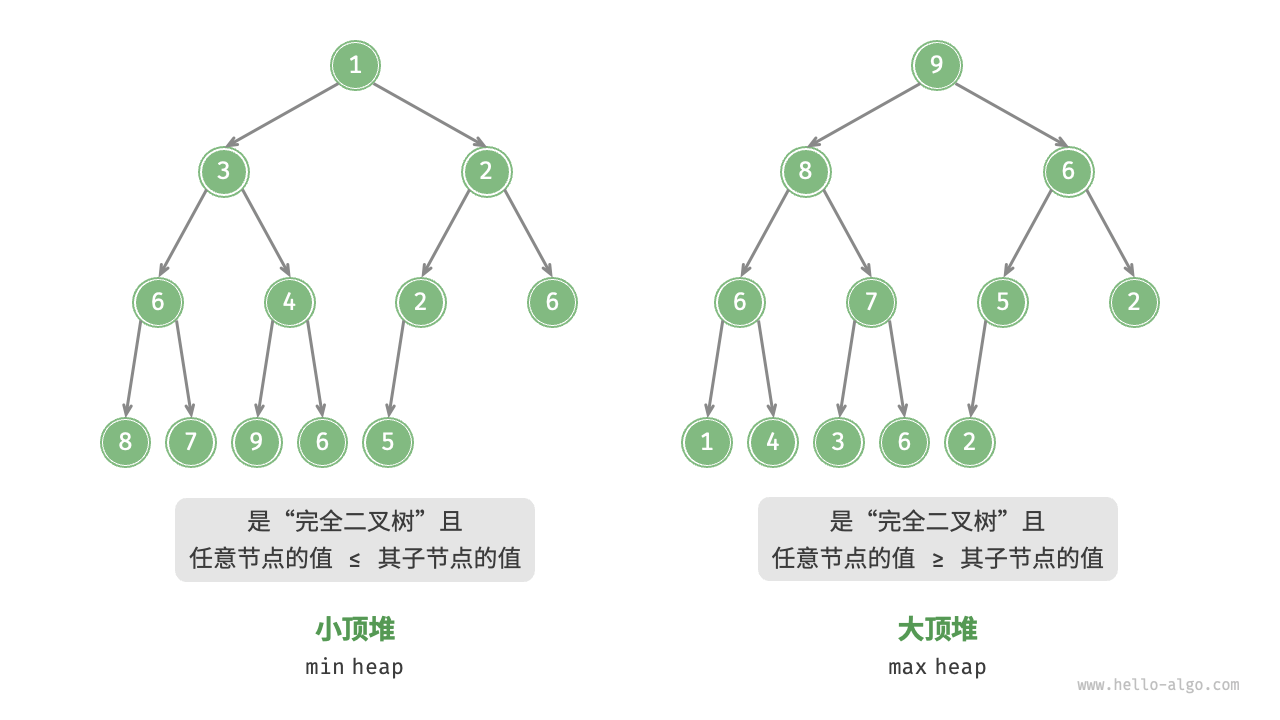
堆(heap)：是一种满足特定条件的完全二叉树，主要分为两种类型，如下：

• 大顶堆：任意节点的值 >= 其子节点的值。
• 小顶堆：任意节点的值 <= 其子节点的值。

堆作为完全二叉树的特例，具有以下特性：

1. 最底层节点靠左填充，其它层的节点都被填满。
2. 我们将堆的二叉树根节点称为堆顶，底层最靠右的节点称为堆底。
3. 对于大顶堆(小顶堆)，根节点堆顶元素的值分别是最大值(最小值)。

堆常见操作和实现

堆通常用来实现优先队列，大顶堆相当于元素从大到小的顺序出队的优先队列，从使用角度讲，优先队列和堆相同的数据结构。

堆的常见操作如下：

• push()：元素入堆。
• pop()：堆顶元素出堆。
• peek()：访问堆顶元素。
• size()：获取堆的元素数量。
• isEmpty()：判断堆是否为空。
• left()：获取左子节点索引。
• right()：获取右子节点索引。
• parent()：获取父节点索引。
• swap()：交换两个节点的值。
• siftUp()：向上堆化。
• siftDown()：向下堆化。

完整代码请参考，基于数组实现的大顶堆。

堆的常见应用

• 优先队列： 堆通常作为实现优先队列的首选数据结构，其入队和出队操作的时间复杂度均为O(logn)，而建队操作为O(n)，这些操作都非常高效。
• 堆排序：给定一组数据，我们可以用它们建立一个堆，然后不断地执行元素出堆操作，从而得到有序数据。
• 获取最大的第K个元素；这是一个经典的算法问题，同时也是一种典型应用，例如选择热度前 10 的新闻作为微博热搜，选取销量前 10 的商品等。

Top K问题

TIP

问题：给定一个长度为N的无序数组，请返回数组中前K大的元素。

实现Top K问题，有以下几种方案，其对比如下：

• 遍历：其解决问题思路是在第1轮找到第一大的元素，第2轮找到第二大的元素，K越趋近于N，效率越差，时间复杂度为O(n²)。
• 排序：先对数组进行完整从大到小(从小到大)排序，再返回前K个元素或后K个元素，其时间复杂度为O(nlogn)。
• 堆：基于小顶堆的特性，高效完成Top K问题。时间复杂度范围为O(n) ~ O(nlogn)

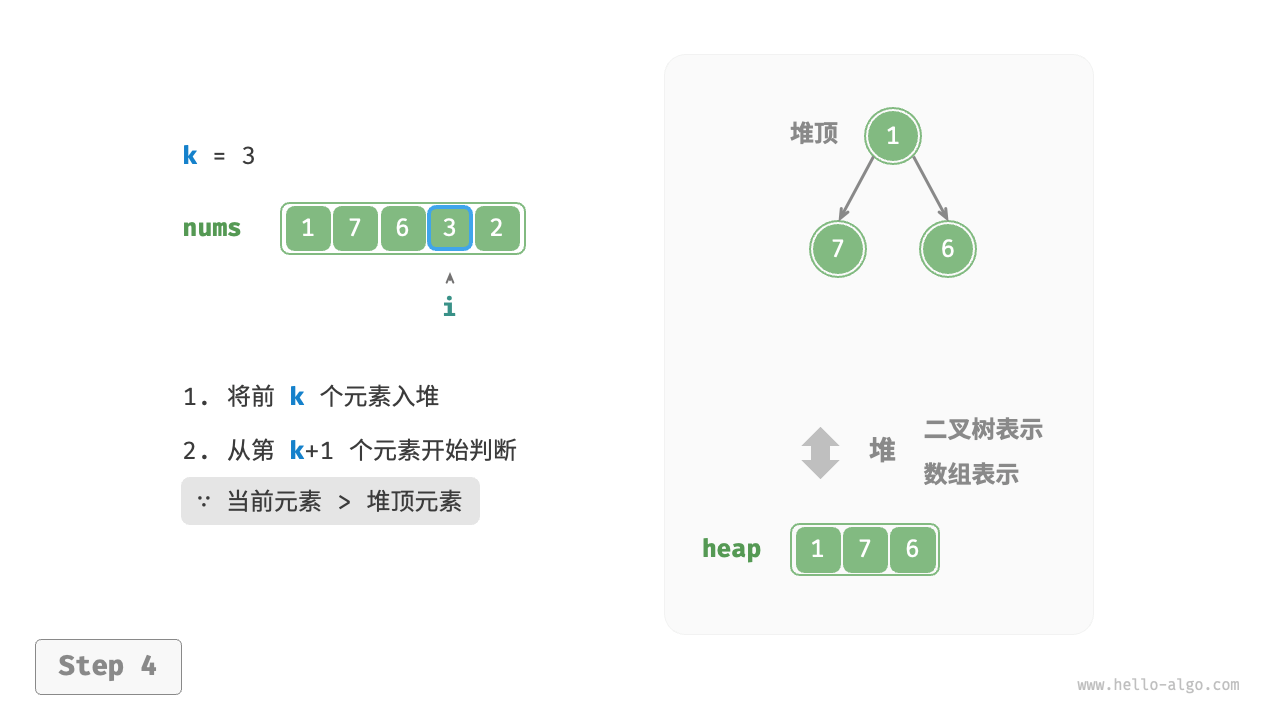
基于小顶堆解决Top K问题的思路如下：

1. 初始化一个小顶堆，其堆顶元素值最小。
2. 先将数组前K个元素依次入堆。
3. 从第K + 1个元素开始，如果当前元素大于堆顶元素，则将堆顶元素出堆，并将当前元素入堆。
4. 遍历完成后，堆中保存的就是最大的K个元素。

完整代码请参考，基于小顶堆实现Top K问题。