搜索

二分查找

二分查找Binary Search，是一种基于分治策略的高效搜索算法。它利用数据的有序性，每轮缩小一半的搜索范围，直至找到目标元素或者搜索区间为空为止。

二分查找

例如，有如下问题：给定一个长度为N的数组nums，元素按从小到大的排列顺序且不重复。请查找并返回元素target在该数组中的索引位置。如数组不包含该元素，则返回-1。

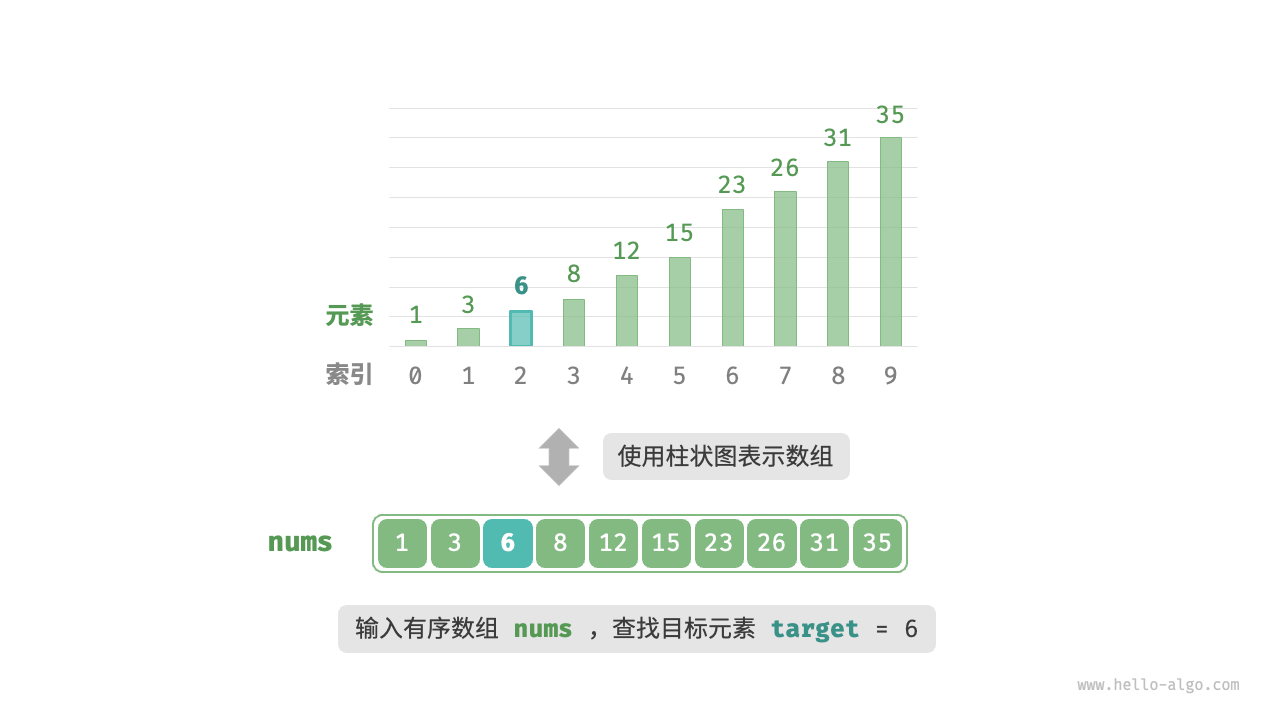
按照二分查找思想，其步骤如下：

1. 初始化指针i和j = n - 1，分别指向数组首元素和尾元素，其初始搜索区间表示为[0, n - 1]。
2. 计算区间的中点索引，m = (i + j) / 2，其中m的值向下取整。考虑到存在大数相加超出取值范围的风险，中点索引计算逻辑调整为：m = i + (j - i) / 2。
3. 判断nums[m]和target的关系，分为三种情况。

• nums[m] < target：说明目标元素在[m + 1, j]的索引区间内，执行i = m + 1。
• nums[m] > target：说明目标元素在[i, m - 1]的索引区间内，执行j = m - 1。
• nums[m] = target：说明找到了目标元素，返回m即可。

4. 若数组不包含目标元素，则最终搜索区间会缩小为空，返回-1。

// 时间复杂度：O(logn)，每轮缩小一半的搜索范围
// 空间复杂度：O(1)，仅定义常量指针
export default function binarySearch(nums, target) {
  let i = 0;
  let j = nums.length - 1;
  while(i <= j) {
    const m = Math.floor(i + (j - i) / 2);
    const val = nums[m];
    if (val < target) {
      i = m + 1;
    } else if (val > target) {
      j = m - 1;
    } else {
      return m;
    }
  }
  return -1;
}

二分查找的局限性

优势：

• 二分查找在数据量大的情况下，查找效率十分的高，因为其时间复杂度为O(logn)。
• 二分查找无须额外空间，相较于需要借助额外空间的搜索算法(例如，哈希表查找)，二分查找更加节省空间。

不足：

• 二分查找仅适用于有序数据，若输入数据无序，为了使用二分查找而专门进行排序，而排序算法通常时间复杂度为O(nlogn)，得不偿失。
• 二分查找仅适用于数组，不适用应用与链表或者基于链表的数据结构。
• 小数据量下，线性查找的性能反而更佳，因为二分查找中有加法、除法、判断等操作。

二分查找的插入点

二分查找不仅适用于查找目标元素，还可用于解决许多变种问题，例如搜索目标元素的插入位置。

示例：给点一个长度为N的有序数组nums和一个元素target，数组不存在重复元素。现需要将target插入数组nums中，并保持其有序性。若数组中已存在元素target，则插入到其左侧。请返回插入后target在新数组中的索引位置。

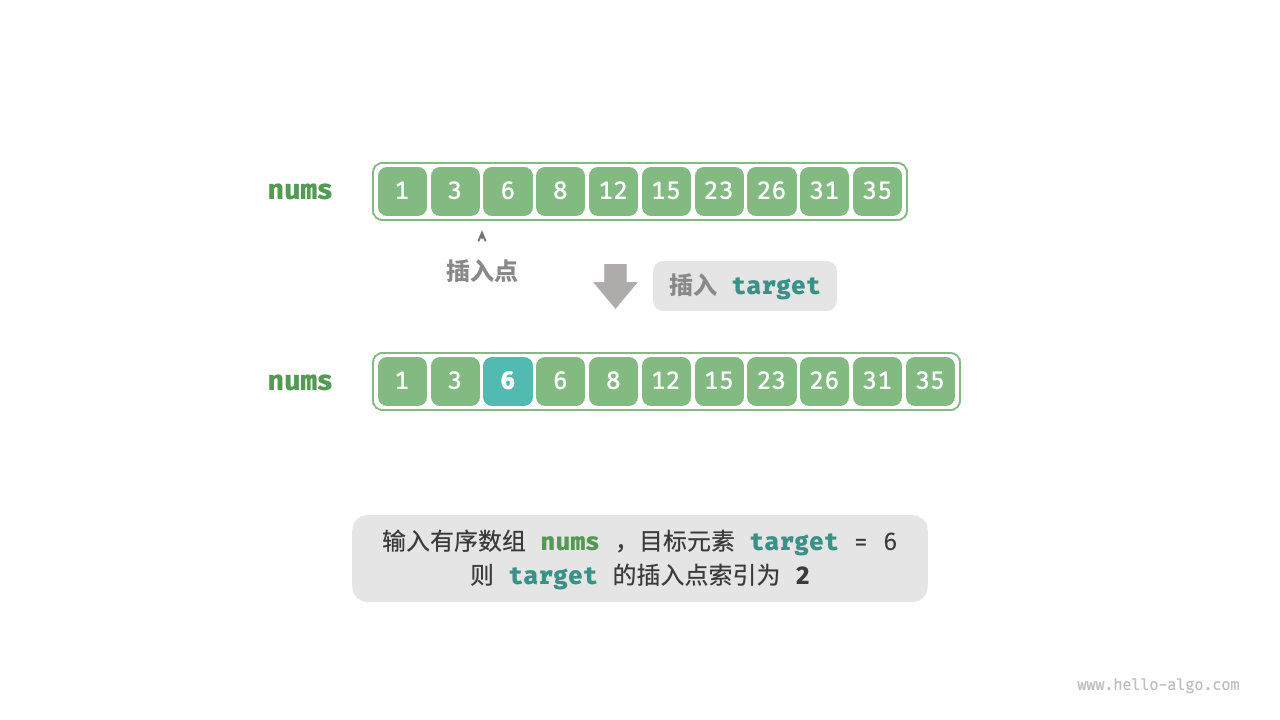
// 不存在target时，i的位置即最终插入位置
// 已存在target时，当循环完毕后，i指向第一个大于target的值，即i也为最终插入位置。
export default function binarySearchIntersectionSimple(nums, target) {
  let i = 0;
  let j = nums.length - 1;
  while(i <= j) {
    const m = Math.floor(i + (j - i) / 2);
    const val = nums[m];
    if (val < target) {
      i = m + 1;
    } else if (val > target) {
      j = m - 1;
    } else {
      return m;
    }
  }
  return i;
}

新要求：在以上题不变的情况下，规定数组包含重复元素。

思路：

• 当nums[m] < target或nums[m] > target时，此时还没有找到target，则继续使用二分法查找。
• 当nums[m] === target时，证明已经找到了target其中一个目标位置，即在[i, m - 1]的区间内，沿用二分查找的思路继续，直至搜索区间为空，此时i即为最终插入位置。

export default function binarySearchIntersection(nums, target) {
  let i = 0;
  let j = nums.length - 1;
  while(i <= j) {
    const m = Math.floor(i + (j - i) / 2);
    const val = nums[m];
    if (val < target) {
      i = m + 1;
    } else if (val > target) {
      j = m - 1;
    } else {
      j = m - 1;
    }
  }
  return i;
}

二分查找边界

与二分查找的插入点类似，在nums元素存在重复的情况下，可以找到target目标元素的左边界和右边界。

查找左边界

示例：给点一个长度为N的有序数组nums，其中可能包含重复元素。请返回数组中最左一个元素target的索引，若数组不包含target目标元素，则返回-1。

查找target的左边界，其本质就是找其插入点。

import binarySearchIntersection  from './binarySearchIntersection.js';

export default function binarySearchLeftEdge(nums, target) {
  const i = binarySearchIntersection(nums, target);
  if (i === nums.length || nums[i] !== target) {
    return -1;
  }
  return i;
}

查找右边界

示例：给点一个长度为N的有序数组nums，其中可能包含重复元素。请返回数组中最右一个元素target的索引，若数组不包含target目标元素，则返回-1。

查找target的右边界，本质就是找其target + 1的插入点，因此可以服用查找左边界的代码。

import binarySearchIntersection  from './binarySearchIntersection.js';

export default function binarySearchRightEdge(nums, target) {
  const i = binarySearchIntersection(nums, target + 1);
  const j = i - 1;

  if (j === -1 || nums[i] !== target) {
    return -1;
  }
  return j;
}

重识搜索算法

搜索算法：用于在数据结构(例如数组、链表、树和图)中搜索一个或者一组满足特定条件的元素。

搜索算法可根据实现思路分为以下两类：

• 通过遍历数据结构来定位目标元素，例如：数组、链表、树和图的遍历。
• 利用数组组织结构或数据包含的先验信息，实现高效元素查找，例如二分查找，哈希查找和二叉搜索树查找等。

暴力搜索

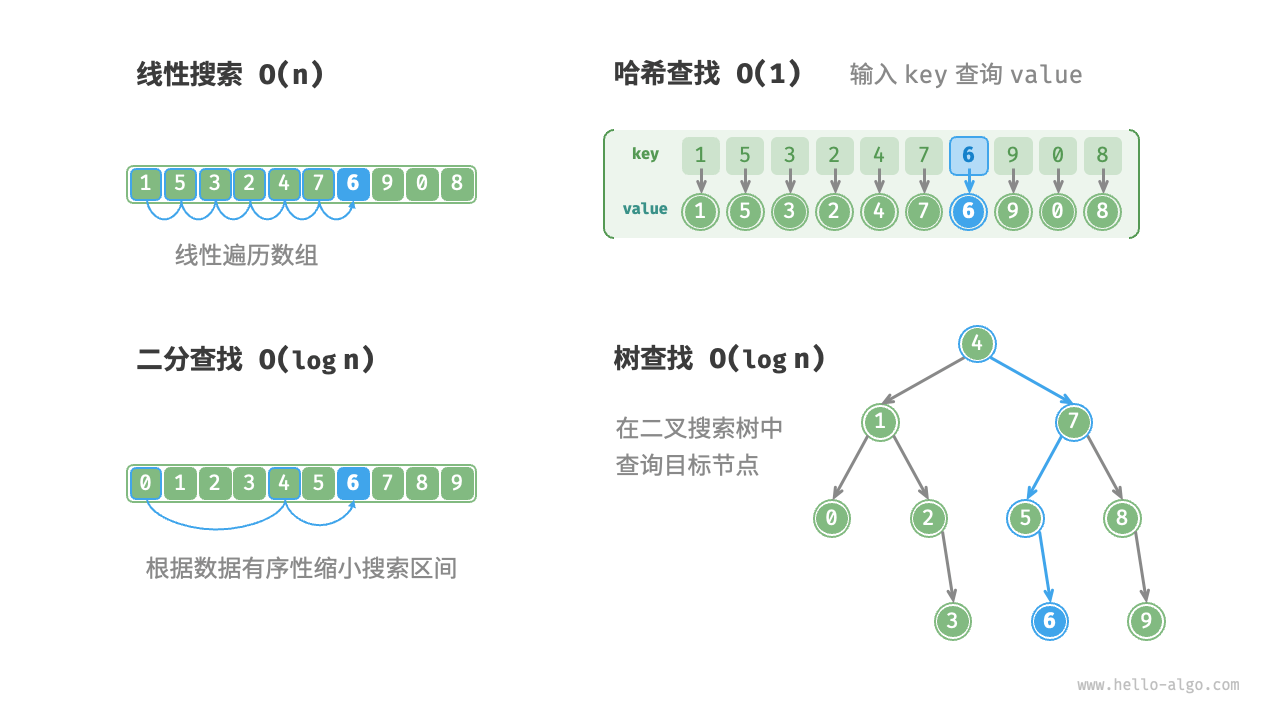
暴力搜索：通过遍历数据结构中的每一个元素来定位目标元素，此类算法的时间复杂度通常为O(n)。

• 线性搜索适用于数组和链表等线性数据结构，它从数据结构的一端开始，逐个访问元素，直到找到目标元素或者到达另外一端仍然没有找到目标元素为止。
• 广度优先搜索和深度优先搜索是图和树的两种遍历策略。广度优先搜索从初始节点开始逐层搜索，由近及远的访问各个节点。深度优先搜索从初始节点开始，沿着一条路径走到头，再回溯并尝试其它路径，直到遍历完整个数据结构。

自适应搜索

自适应搜素：利用数据的特有属性来优化搜索过程，从而高效的定位目标元素，此类算法的优点是效率高，时间复杂度通常可达O(logn)或者O(1)。

• 二分查找：利用数据的有序性实现高效查找，仅适用于数据。
• 哈希查找：利用哈希表将搜索数据和目标数据建立为键值对映射，从而实现查询操作(空间换时间)。
• 树查找：在特定的树结构(例如，二叉搜索树)中，基于比较节点的值来快速排除节点，从而定位目标元素。

搜索算法选取

以上各个搜索算法的原理如下：

操作	线性搜索	二分查找	树查找	哈希查找
查找元素	O(n)	O(logn)	O(logn)	O(1)
插入元素	O(1)	O(n)	O(logn)	O(1)
删除元素	O(n)	O(n)	O(logn)	O(1)
额外空间	O(1)	O(1)	O(n)	O(n)
数据预处理	/	排序O(nlogn)	建树O(nlogn)	建哈希表O(n)
数据是否有序	否	是	是	否

搜索算法的选择还取决于数据体量、搜索性能要求、数据查询与更新频率等。

线性搜索

• 通用性较好，无须任何数据预处理操作。假如我们仅需查询一次数据，那么其他三种方法的数据预处理的时间比线性搜索的时间还要更长。
• 适用于体量较小的数据，此情况下时间复杂度对效率影响较小。
• 适用于数据更新频率较高的场景，因为该方法不需要对数据进行任何额外维护。

二分查找

• 适用于大数据量的情况，效率表现稳定，最差时间复杂度为O(logn)。
• 数据量不能过大，因为存储数组需要连续的内存空间。
• 适用于高频增删数据的场景，因为维护有序数组的开销较大。

哈希查找

• 适合对查询性能要求很高的场景，平均时间复杂度为O(1)。
• 不适合需要有序数据或范围查找的场景，因为哈希表无法维护数据的有序性。
• 对哈希函数和哈希冲突处理策略的依赖性较高，具有较大的性能劣化风险。
• 不适合数据量过大的情况，因为哈希表需要额外空间来最大程度地减少冲突，从而提供良好的查询性能。

树查找

• 适用于海量数据，因为树节点在内存中是分散存储的。
• 适合需要维护有序数据或范围查找的场景。
• 在持续增删节点的过程中，二叉搜索树可能产生倾斜，时间复杂度劣化至O(n)。
• 若使用 AVL 树或红黑树，则各项操作可在O(logn)效率下稳定运行，但维护树平衡的操作会增加额外的开销

参考

• Hello 算法 搜索