排序
排序算法
排序算法(Sorting Algorithm):用于对一组数据按照特定的顺序进行排序。排序算法有着广泛的应用,因为有序的数据通常能够被高效的查找、分析和处理。
排序算法的评价维度如下:
- 运行效率:排序算法的时间复杂度尽量低,且总体操作数量较少(时间复杂度中的常数项变小)。
- 就地性:不借助辅助数组,直接在原数组上操作,进而实现排序的目的。通常情况下,原地排序的数据搬运操作较少,运行速度也更快。
- 稳定性:完成排序后,相等元素在数组中的相对顺序不发生变化。
- 自适应性:自适应性的时间复杂度会受输入数据的影响,即最佳时间复杂度、最差时间复杂度、平均时间复杂度并不完全相等。
- 是否基于比较:基于比较的排序,依赖比较运算符(<、>和=)来判断元素的相对顺序,从而排序整个数组,理论最优时间复杂度为
O(nlogn)。而非比较排序不使用比较运算符、时间复杂度可达O(n),但其通用性相对较差。
选择排序
选择排序(Selection Sort),其工作原理是:开启一个循环,每轮从未排序的区间选择最小的元素,将其放到已排序区间的末尾。
选择排序其算法特性如下:
- 时间复杂度
O(n²),非自适应排序。 - 空间复杂度
O(1),原地排序。 - 非稳定性排序,值相同的两个元素有可能会被改变其相对顺序。
function selectionSort(nums) {
let n = nums.length;
// 外层循环,未排序区间
for(let i = 0; i < n - 1; i++) {
let k = i;
// 内层循环,在未排序区间中选择值最小的
for(let j = i + 1; j < n; j++) {
if (nums[j] < nums[i]) {
k = j;
}
}
// 将最小元素和未排序区间的首个元素互换(已排序区间末尾)
[nums[i], nums[k]] = [nums[k], nums[i]];
}
return nums;
}
冒泡排序
冒泡排序(Bubble Sort):通过连续地比较与交换相邻元素实现排序。这个过程就像气泡从底部升到顶部一样,因此叫冒泡排序。
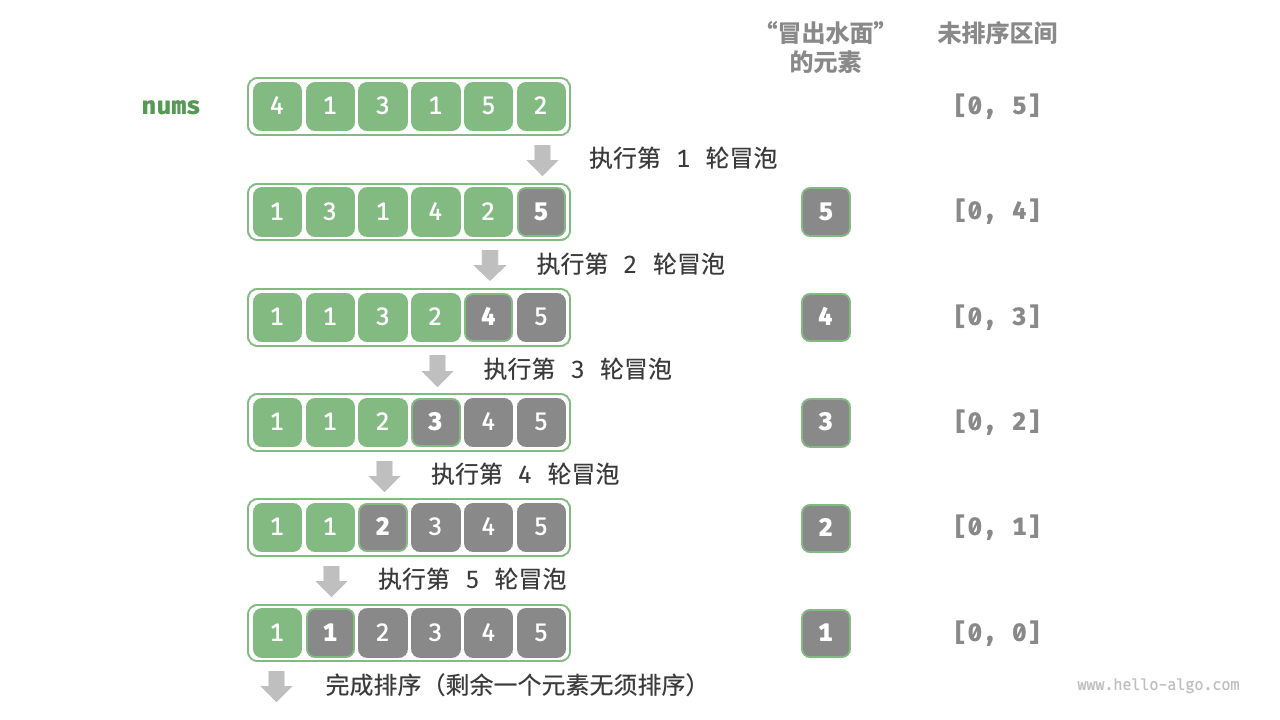
冒泡排序其算法特性如下:
- 时间复杂度
O(n²),自适应排序。 - 空间复杂度
O(1),原地排序。 - 稳定排序,冒泡过程中相同元素不交换。
function bubbleSort(nums) {
// 外层循环:未排序区间[0, n]
for(let i = nums.length - 1; i >= 0; i--) {
// 内层循环:将未排序区间中最大的元素,交换到该区间的最右侧。
for (let j = 0; j < i; j++) {
if (nums[j] > nums[j + 1]) {
[nums[j], nums[j + 1]] = [nums[j + 1], nums[j]];
}
}
}
return nums;
}
插入排序
插入排序(Insertion Sort):是一种简单的排序算法,它的工作原理与手动整理一副牌的过程非常相似。具体来说,我们在未排序区间选择一个基准元素,将该元素与其左侧已排序区间的元素逐一比较大小,并将其插入到正确的位置。
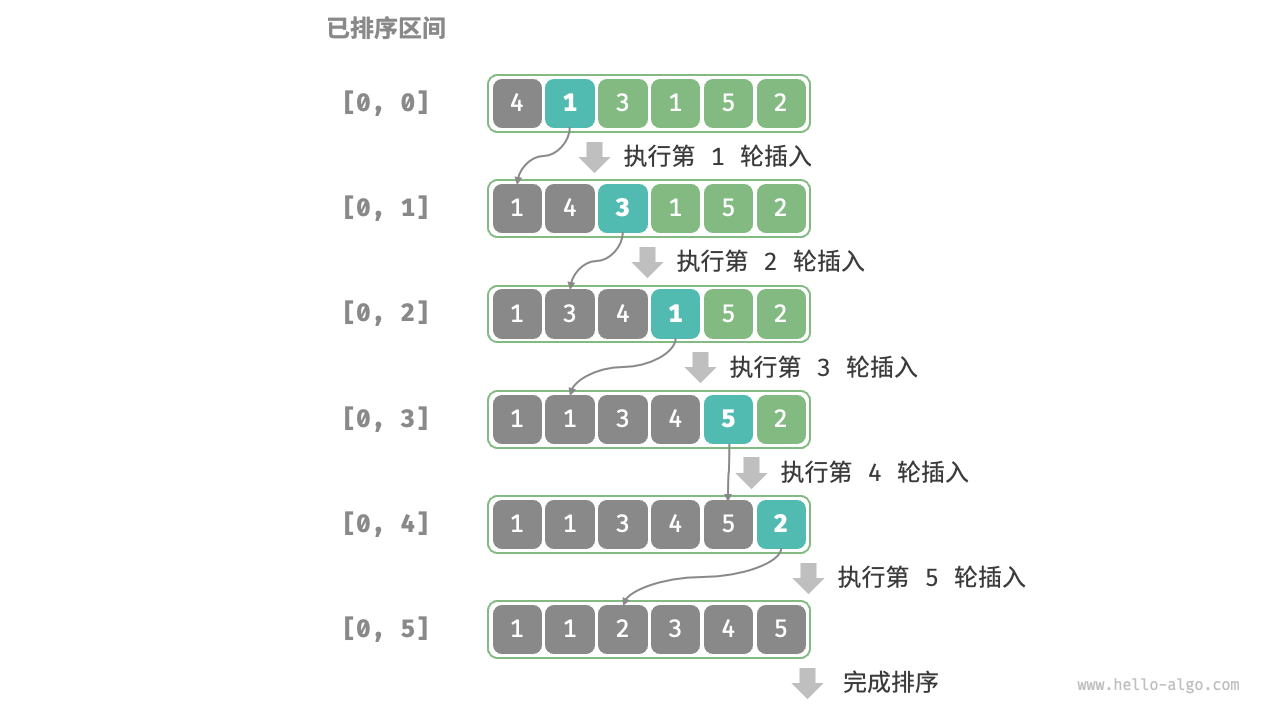
插入排序其算法特性如下:
- 时间复杂度
O(n²),自适应排序。 - 空间复杂度
O(1),原地排序。 - 稳定排序:在排序过程中,我们会将元素插入到相同元素的右侧,不会改变它们的顺序。
function insertionSort(nums) {
// 外层循环:已排序元素数量
for(let i = 1; i < nums.length; i++) {
const base = nums[i];
let j = i - 1;
// 内层循环:将base插入到已排序部分的正确位置
while(j >= 0 && nums[j] > base) {
nums[j + 1] = nums[j];
j--;
}
nums[j + 1] = base;
}
return nums;
}
快速排序
快速排序(Quick Sort):是一种基于分治策略的排序算法,其运行高效,应用广泛。快速排序的核心操作是哨兵划分,其目标是:选择数组中某个元素为基准数,将所有小于基准数的元素移到其左侧,而大于其基准数的元素移到其右侧
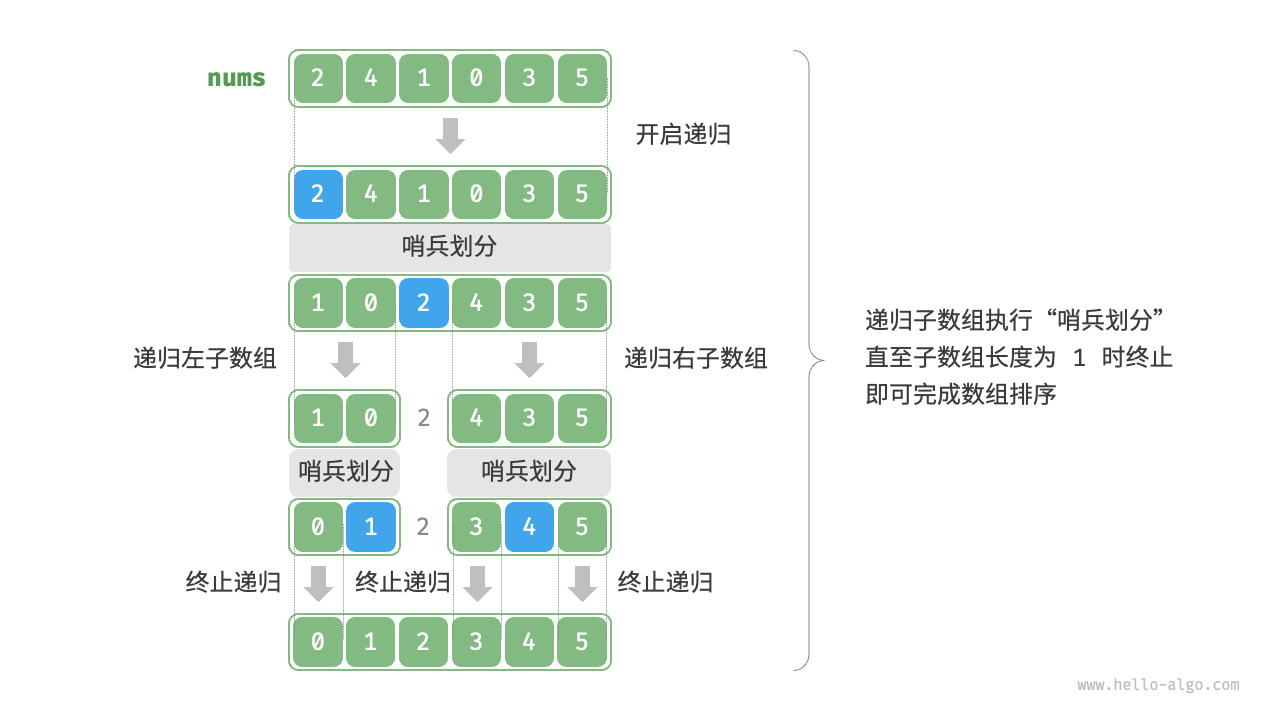
快速排序其算法特性:
- 时间复杂度
O(nlogn),自适应排序。 - 时间复杂度
O(n),原地排序。 - 非稳定性排序,在哨兵划分的最后一步,基准数可能会被交换至相等元素的右侧。
快速排序为什么快:
- 出现最差情况的概率很低:在大多数情况下,快速排序能在
O(nlogn)的时间复杂度下运行。 - 缓存使用效率高:在执行哨兵划分操作时,系统可将整个子数组加载到缓存,因此访问元素的效率较高。而像堆排序这类算法需要跳跃式访问元素,从而缺乏这一特性。
- 复杂度的常数系数小:快速排序的比较、赋值、交换等操作的总数量最少。
常规实现:
// 交换两个元素的值
function swap(nums, i, j) {
const temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
// 快速排序哨兵划分
function partition(nums, left, right) {
let i = left;
let j = right;
while(i < j) {
while(i < j && nums[j] >= nums[left]) {
j--;
}
while(i < j && nums[i] <= nums[left]) {
i++;
}
swap(nums, i, j);
}
swap(nums, i, left);
return i;
}
function quickSort(nums, left, right) {
if (left >= right) {
return;
}
const pivot = partition(nums, left, right);
quickSort(nums, left, pivot - 1);
quickSort(nums, pivot + 1, right);
return nums;
}
基准数优化:快速排序在某些输入下的时间效率可能降低,例如输入数组完全是倒序的,此时分治策略生效,快速排序退化为冒泡排序。此种情况下,可以优化划分哨兵中基准数的选取策略。
// 三个树取其中位数
function median(nums, left, mid, right) {
if ((nums[left] < nums[mid]) ^ (nums[left] < nums[right])) {
return left
} else if ((nums[mid] < nums[left]) ^ (nums[mid] < nums[right])) {
return mid
} else {
return left
}
}
// 快速排序哨兵划分
function partition(nums, left, right) {
let mid = median(nums, left, Math.floor((left + right) / 2), right)
swap(nums, left, mid)
let i = left;
let j = right;
while(i < j) {
while(i < j && nums[j] >= nums[left]) {
j--;
}
while(i < j && nums[i] <= nums[left]) {
i++;
}
swap(nums, i, j);
}
swap(nums, i, left);
return i;
}
尾递归优化:在某些输入下,快速排序可能占用的内存空间较多。为了防止栈帧空间的积累,我们可以在每轮哨兵排序完毕后,比较两个子数组的长度,仅对较短的子数组进行递归。
function quickSort(nums, left, right) {
if (left >= right) {
return;
}
const pivot = partition(nums, left, right);
if (pivot - left < right - pivot) {
quickSort(nums, left, pivot - 1)
left = pivot + 1
} else {
quickSort(nums, pivot + 1, right);
right = pivot - 1
}
return nums;
}
归并排序
归并排序(Merge Sort):是一种基于分治策略的排序算法,主要包含划分和合并两个阶段。
- 划分阶段:通过递归不断的将数组从中心处分开,将长数组的排序问题转换为短数组的排序问题。
- 合并阶段:当子数组长度为1时终止划分,开始合并,持续的将左右两个较短的有序数组合并为一个较长的有序数组,直至结束。
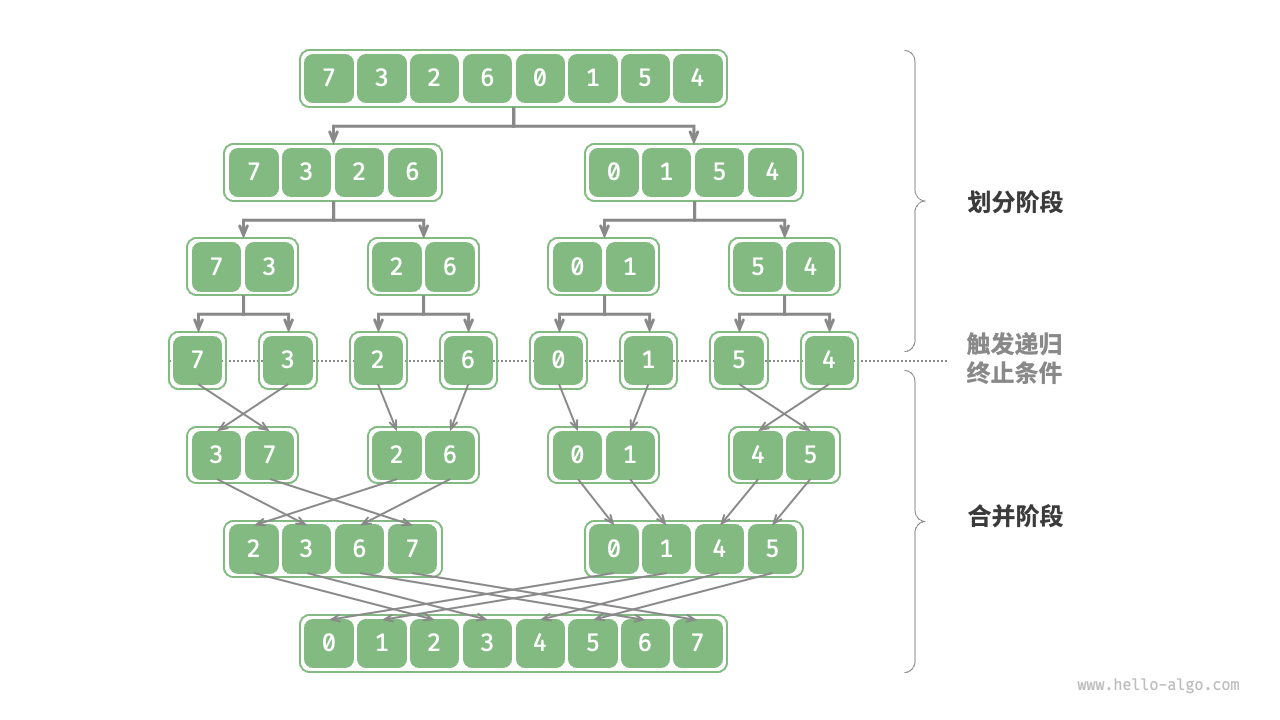
归并排序其算法特性:
- 时间复杂度为
O(nlogn),非适应性排序。划分产生O(logn)的递归树,合并的总操纵数为O(n)。 - 空间复杂度为
O(n),非原地排序。合并需要借助辅助数组实现,使用O(n)大小的额外空间。 - 稳定排序。
function merge(nums, left, mid, right) {
let temp = new Array(right - left + 1);
let i = left;
let j = mid + 1;
let k = 0;
// 依次比较左、右两个数组中的元素
while(i <= mid && j <= right) {
if (nums[i] <= nums[j]) {
temp[k++] = nums[i++];
} else {
temp[k++] = nums[j++];
}
}
// 如果左数组中还有元素
while(i <= mid) {
temp[k++] = nums[i++];
}
// 如果右数组中还有元素
while(j <= right) {
temp[k++] = nums[j++];
}
// 临时数组中的元素赋值到原数组
for(let k = 0; k < temp.length; k++) {
nums[left + k] = temp[k];
}
}
function mergeSort(nums, left, right) {
if (left >= right) {
return;
}
const mid = Math.floor((left + right) / 2);
// 左数组划分
mergeSort(nums, left, mid);
// 右数组划分
mergeSort(nums, mid + 1, right);
// 左、右有序数组合并
merge(nums, left, mid, right);
return nums;
}
堆排序
堆排序(Heap Sort):是一种基于堆数据结构实现的高效排序算法,堆数据结构主要包含元素建堆操作和元素出堆操作。
堆排序其算法特性如下:
- 时间复杂度
O(nlogn),非自适应排序。建堆操作O(n),从堆中提取最大元素的时间复杂度为O(logn)。 - 空间复杂度
O(1),原地排序。 - 非稳定排序,交换堆顶和堆底元素时,相等元素的相对位置可能发生变化。
function siftDown(nums, n, i) {
while(true) {
const left = i * 2 + 1;
const right = i * 2 + 2;
let max = i;
if (left < n && nums[left] > nums[max]) {
max = left;
}
if (right < n && nums[right] > nums[max]) {
max = right;
}
if (max === i) {
break;
}
[nums[max], nums[i]] = [nums[i], nums[max]];
i = max;
}
}
function heapSort(nums) {
const len = nums.length;
// 建堆
for(let i = Math.floor(len / 2) - 1; i >= 0; i--) {
siftDown(nums, len, i);
}
// 从堆中取最大元素,循环n - 1轮
for(let i = len - 1; i > 0; i--) {
// 交换堆顶和堆底元素
[nums[0], nums[i]] = [nums[i], nums[0]];
// 从根节点开始,重新进行堆化
siftDown(nums, i, 0);
}
return nums
}
桶排序
桶排序(Bucket Sort):非比较元素大小方式实现的排序,是一种分治策略的典型应用。它通过设置一些具有大小顺序的桶,每个桶对应一个数据范围,将数据平均分配到各个桶中。然后,在每个桶内部分别执行排序,最终按照桶的顺序将所有数据合并。
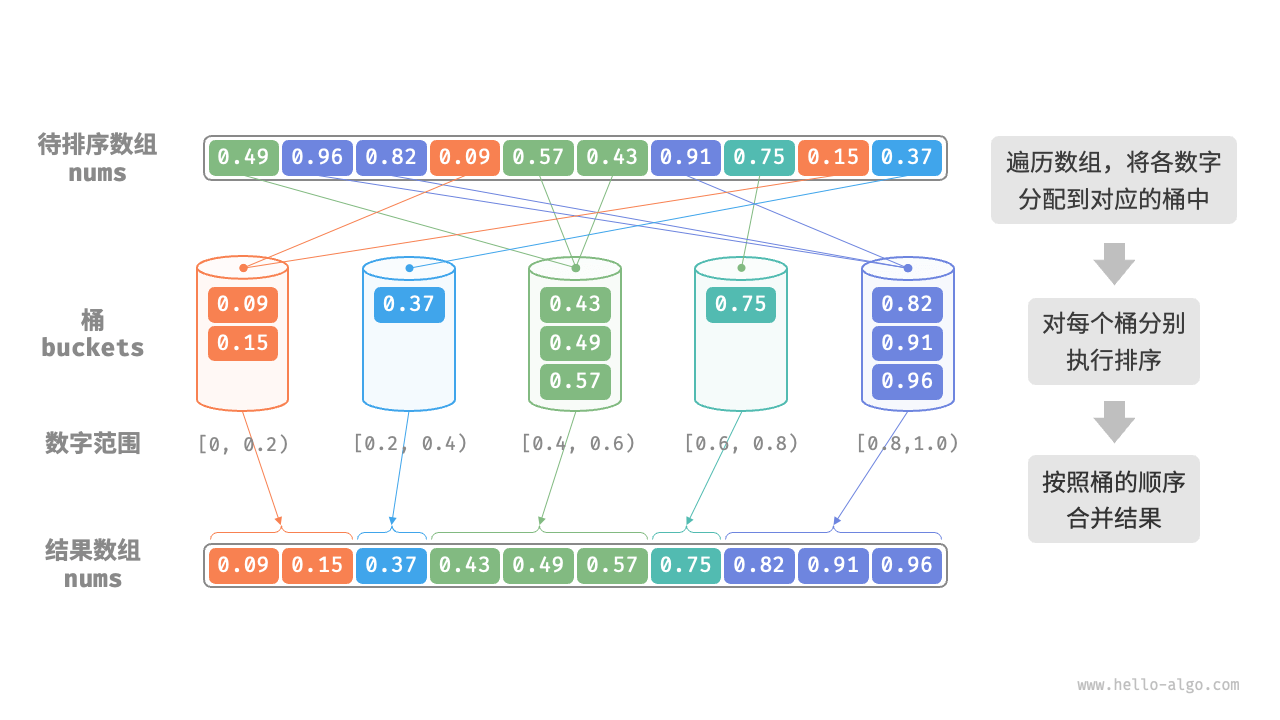
桶排序算法其算法特性如下:
- 非常适合用来处理体量很大的数据。
- 时间复杂度
O(n + k),拆分元素到桶中且排序时间复杂度为O(n),合并所有桶中的元素,时间复杂度为O(k),其中k为桶的数量。 - 空间复杂度
O(n + k),非原地排序。 - 桶排序是否稳定取决于排序桶内元素的算法是否稳定。
function bucketSort(nums) {
const len = nums.length;
const k = Math.floor(len / 2);
const buckets = [];
// 初始化桶
for(let i = 0; i < k; i++) {
buckets.push([]);
}
// 元素分桶
for(let i = 0; i < len; i++) {
const num = nums[i];
const index = Math.floor(num * k);
buckets[index].push(num);
}
// 对桶中元素进行排序
for(let i = 0; i < k; i++) {
const bucket = buckets[i];
bucket.sort((a, b) => a - b);
}
// 合并桶中元素
let i = 0;
for(const bucket of buckets) {
for(const num of bucket) {
nums[i++] = num;
}
}
return nums;
}
计数排序
计数排序(Counting Sort):本质是桶排序的一个特例,它通过统计元素数量来实现排序,通常应用于整数数组。
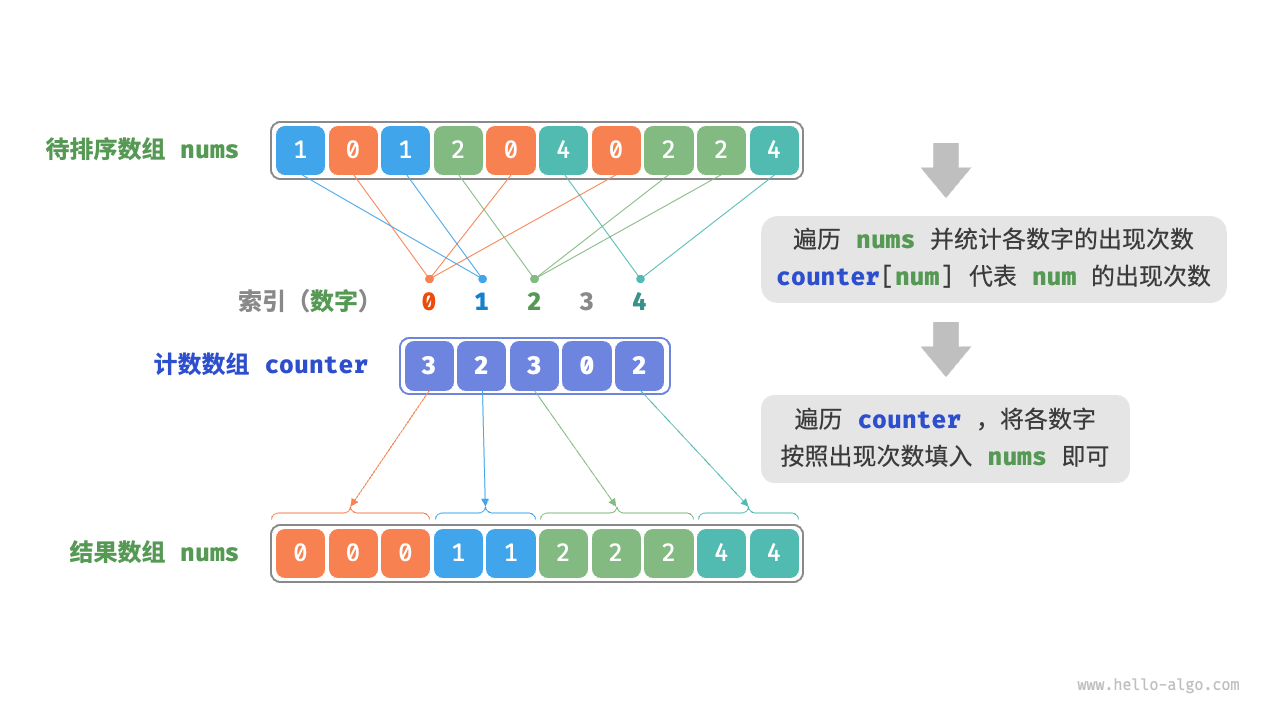
计数排序其算法特性如下:
- 只适用于非负整数。
- 适用于数据量大但数据范围较小的情况。
- 时间复杂度为
O(n + m),n为原始数组中元素数量,m为计数数组中元素数量。 - 空间复杂度为
O(n + m),非原地排序。 - 稳定排序。
function countSort(nums) {
const len = nums.length;
// 统计最大元素
let max = 0;
for(const num of nums) {
max = Math.max(max, num);
}
// 统计各数字出现的次数
const counters = new Array(max + 1).fill(0);
for(const num of nums) {
counters[num]++;
}
// 计算前缀和,将出现次数转换为尾索引
for(let i = 0; i < max; i++) {
counters[i + 1] += counters[i];
}
// 倒序遍历,将各元素填入结果数组res中
const res = []
for(let i = len - 1; i >= 0; i--) {
const num = nums[i];
res[counters[num] - 1] = num;
counters[num]--;
}
// 结果数组res覆盖原始nums数组
for(let i = 0; i < len; i++) {
nums[i] = res[i];
}
return nums;
}
基数排序
基数排序(Radix Sort):其核心思想和计数排序一致,也通过统计个数来实现排序。在此基础上,基数排序利用数字各位之间的递进关系,依次对每一位进行排序,从而得到最终的排序结果。
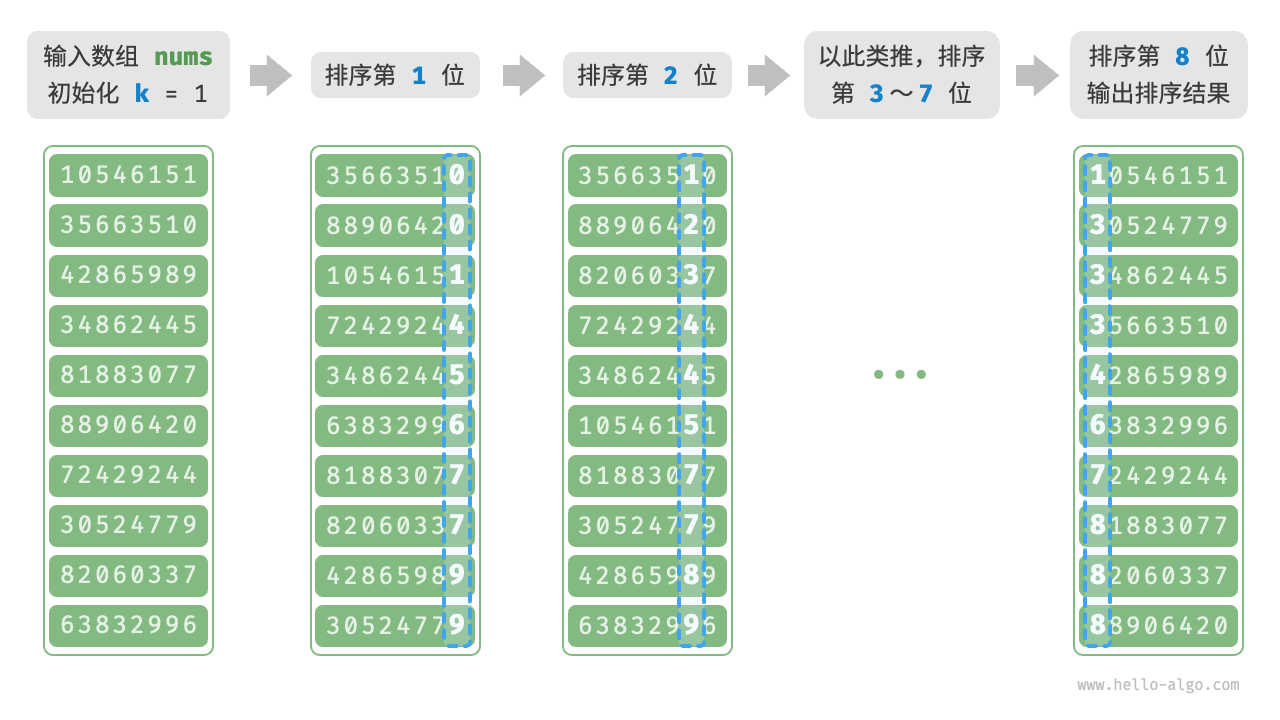
基数排序其算法特性如下:
- 时间复杂度
O(nk),n为数据量,k为最大位数。 - 空间复杂度
O(n + d),非原地排序 - 稳定排序
function digit(num, exp) {
return Math.floor(num / exp) % 10;
}
function countingSortDigit(nums, exp) {
const counter = new Array(10).fill(0);
const n = nums.length;
// 统计 0~9 各数字的出现次数
for (let i = 0; i < n; i++) {
const d = digit(nums[i], exp);
counter[d]++;
}
// 求前缀和,将出现个数转换为数组索引
for (let i = 1; i < 10; i++) {
counter[i] += counter[i - 1];
}
// 倒序遍历,根据桶内统计结果,将各元素填入 res
const res = new Array(n).fill(0);
for (let i = n - 1; i >= 0; i--) {
const d = digit(nums[i], exp);
const j = counter[d] - 1;
res[j] = nums[i];
counter[d]--;
}
// 使用结果覆盖原数组 nums
for (let i = 0; i < n; i++) {
nums[i] = res[i];
}
}
function radixSort(nums) {
// 获取最大值
let max = Number.MIN_VALUE;
for(const num of nums) {
if (num > max) {
max = num;
}
}
// 从低位到高位的顺序遍历
for(let exp = 1; exp <= max; exp *= 10) {
countingSortDigit(nums, exp);
}
return nums;
}