栈和队列

栈

栈Stack是一种遵循先入后出逻辑的线性数据结构。

栈数据结构一般而言有如下几种概念：

1. 栈数据结构的顶部叫做栈顶。
2. 栈数据结构的底部叫做栈底。
3. 移除栈顶元素的过程叫做出栈。
4. 向栈顶添加元素的过程叫做入栈或者压栈。

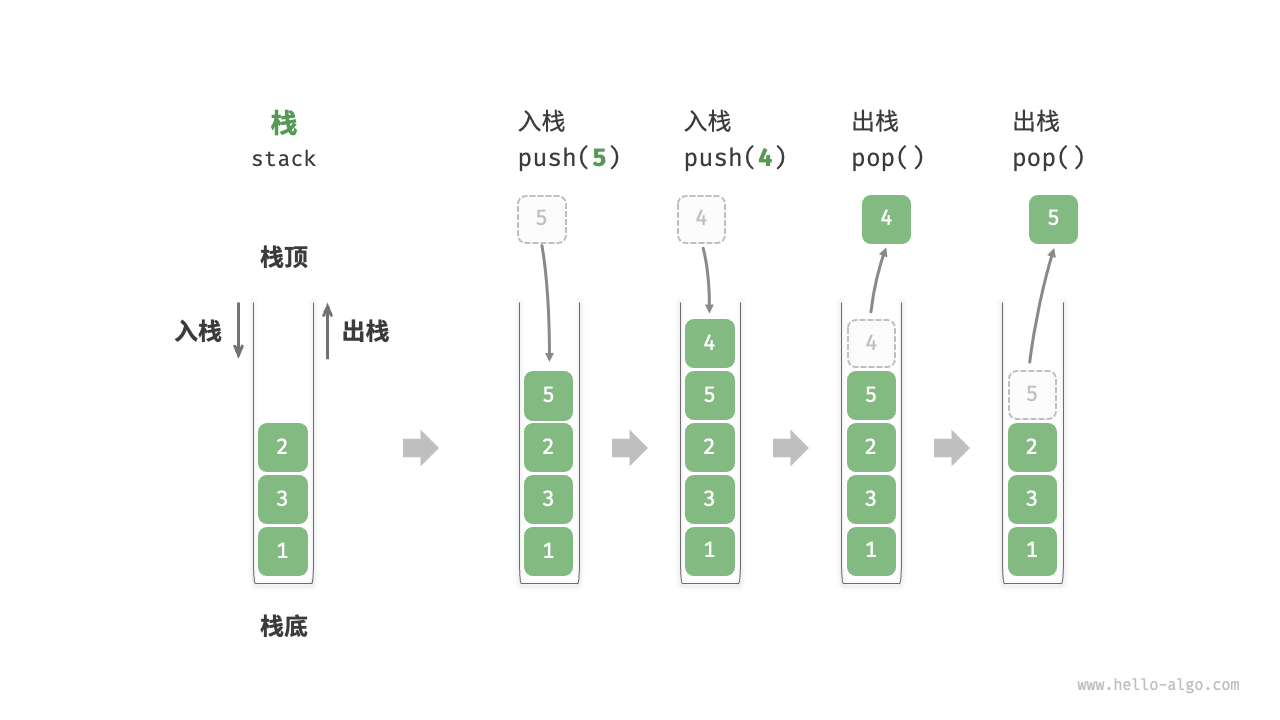
根据以上概念或过程，一般栈有如下几种常见操作：

1. 入栈push()，时间复杂度O(1)。
2. 出栈pop()，时间复杂度O(1)。
3. 访问栈顶元素peek()，时间复杂度O(1)。

根据不同语言的不同特性，栈有不同的实现方式，在JavaScript中，可以使用数组或者链表来实现栈结构。其中栈结构的属性和方法如下：

• push()：向栈顶添加一个元素。
• pop()：移除栈顶元素。
• peek()：访问栈顶元素。
• isEmpty(): 判断栈结构是否为空。
• clear()：清空栈中所有元素。
• getSize(): 获取栈中元素个数。
• toArray()：返回栈数组结构。

栈数组实现

栈的数组实现，请参考ArrayStack

栈的链表实现

栈的链表实现，请参考LinkedListStack

两种实现方式对比

时间效率：

1. 基于数组实现的栈，如果入栈的数量超过初始容量，会触发扩容操作，此时效率会变低，但平均效率高。
2. 基于链表实现的栈，可以提供比较稳定的效率表现。

空间效率：

1. 基于数组实现的栈，在扩容后可能会存在一定的空间浪费。
2. 基于链表实现的栈，需要额外存储节点指针，空间开销相对比较大。

栈的典型应用

• 浏览器的前进，后退；软件中的撤销，反撤销：当打开网页时，会将上一个网页进行入栈操作，这样我们可以通过浏览器的后退功能回到上一页，其中后退操作其实就是出栈。
• 程序内存管理：每次调用函数时，系统都会在栈顶添加一个栈帧，用于记录函数的上下文信息。在递归函数中，向下递推阶段会不断执行入栈操作，而向上回溯阶段则会执行出栈操作。

队列

队列Queue是一种遵循先入先出规则的线性数据结构。

队列数据结构一般而言有如下几种概念：

1. 队列的头部叫做队首。
2. 队列的尾部叫做队尾。
3. 队列的尾部添加元素叫入队。
4. 队列的头部移除元素叫出队。

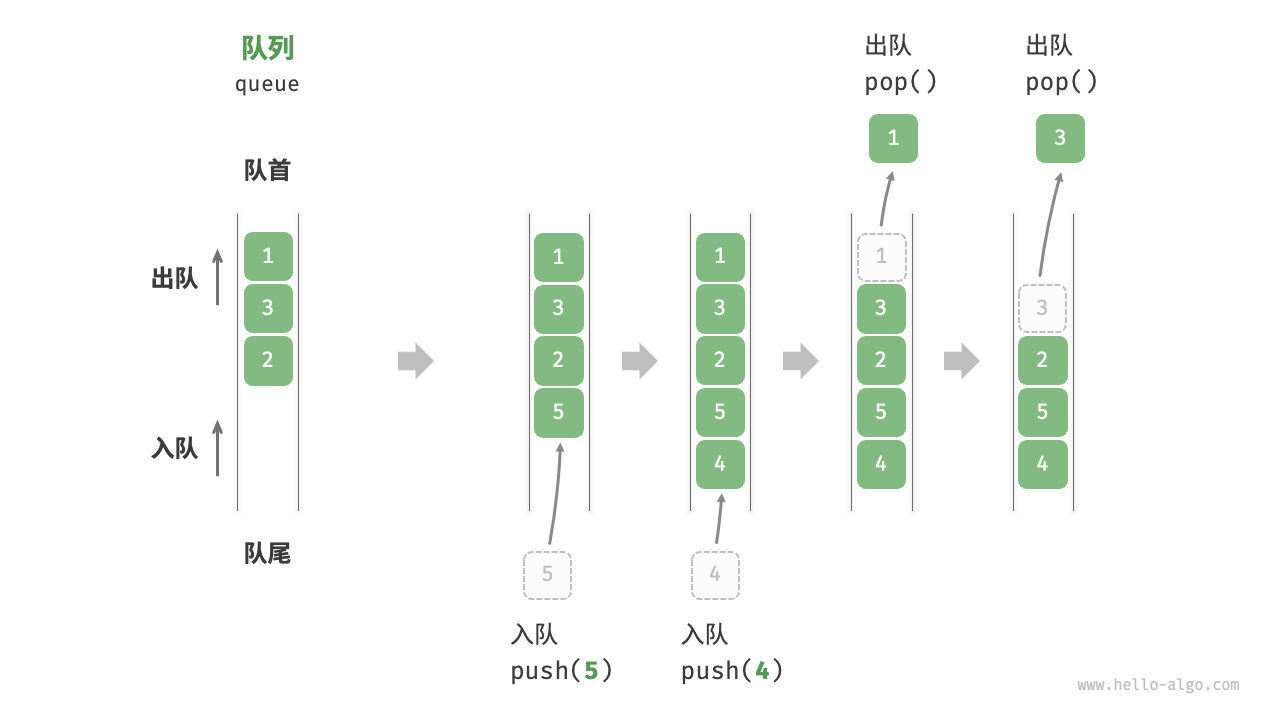
根据以上概念或过程，一般队列有如下几种常见操作：

1. 入队push()，时间复杂度O(1)。
2. 出队pop()，时间复杂度O(1)。
3. 访问队首元素peek()，时间复杂度O(1)。

根据不同语言的不同特性，队列有不同的实现方式，在JavaScript中，可以使用数组或者链表来实现队列结构。其中队列结构的属性和方法如下：

• push()：入队，向队列尾部添加一个元素。
• pop()：出队，移除队首元素。
• peek()：访问队首元素。
• isEmpty(): 判断队列结构是否为空。
• clear()：清空队列中所有元素。
• getSize(): 获取队列元素个数。
• toArray()：返回队列数组结构。

队列数组实现

队列的数组实现，请参考ArrayQueue

队列链表实现

队列的链表实现，请参考LinkedListQueue

队列典型应用

• 购物商城订单：购物者下单后，订单将加入队列中，系统随后会根据顺序依次处理队列中的订单。
• 各类待办事项：任何需要实现“先来后到”功能的场景，例如打印机的任务队列、餐厅的出餐队列等。队列在这些场景中可以有效地维护处理顺序。

双端队列

在队列Queue中，我们仅能在队首删除元素，队尾添加元素。为了增加灵活性，双端队列Dequeue允许我们在队首和队尾添加和删除元素。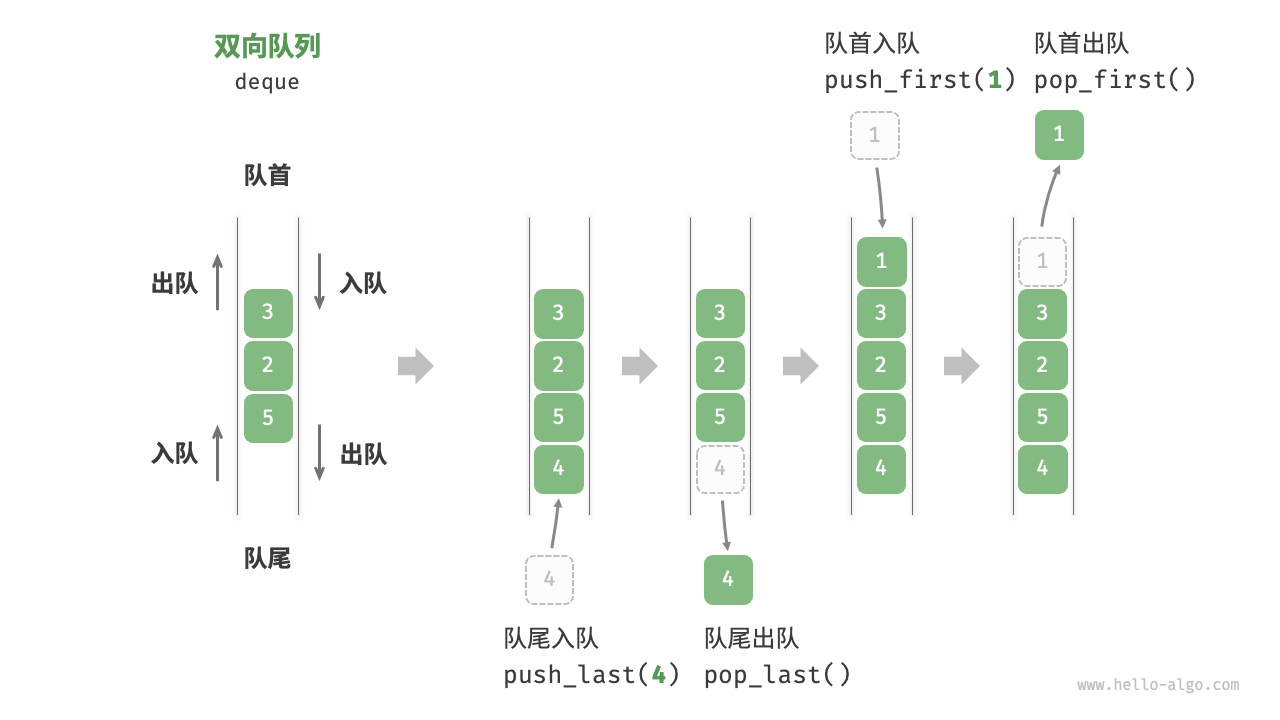

根据双端队列的特性，一般双端队列有如下几种常见操作：

1. 队首入队pushFirst，时间复杂度O(1)。
2. 队尾入队pushLast，时间复杂度O(1)。
3. 队首出队popFirst，时间复杂度O(1)。
4. 队尾出队popLast，时间复杂度O(1)。
5. 访问队首元素peekFirst，时间复杂度O(1)。
6. 访问队尾元素peekLast，时间复杂度O(1)。

双端队列数组实现

双端队列的数组实现，请参考ArrayDequeue

双端队列链表实现

双端队列的链表实现，请参考LinkedListDequeue

双端队列典型应用

双向队列兼具栈与队列的逻辑，因此它可以实现这两者的所有应用场景，同时提供更高的自由度。

许多软件的撤销功能通常使用栈来实现：系统每次将更改操作push到栈中，然后通过pop实现撤销。然而实际场景下，会考虑到系统资源占用情况，例如只存储50次更改操作。超过时，需要在栈底(队首)执行删除操作，但栈是无法做到在栈底执行删除操作的，所以需要使用双端队列来实现。

参考

• Hello 算法 栈和队列