二叉树

二叉树

二叉树是一种非线性数据结构，代表着祖先和后代之间的派生关系，体现着一分为二的分治逻辑。

与链表类似，二叉树的基本单元是节点，其中每个节点包含：根节点、左节点和右节点。

export default class TreeNode {
  constructor(val, left, right) {
    this.val = val;
    this.left = left || null;
    this.right = right || null;
  }
}

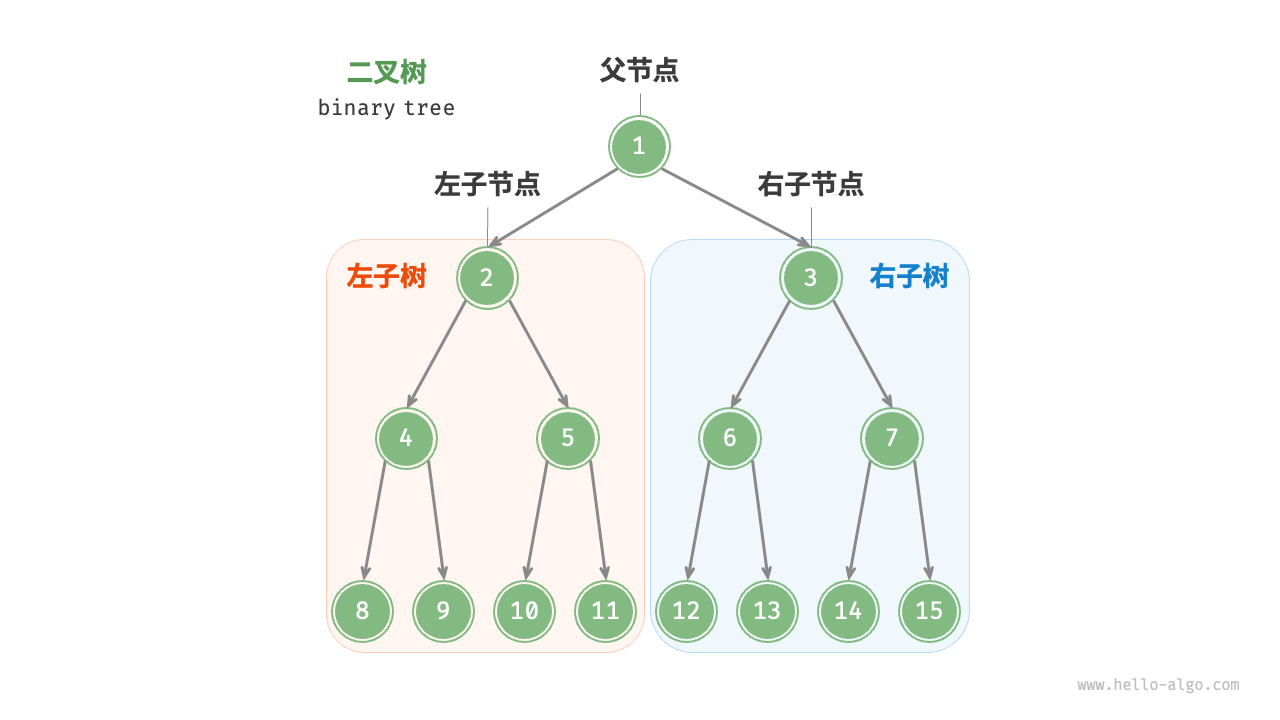
二叉树的常见术语

在二叉树中，一般有如下常见术语：

• 根节点(rootNode): 二叉树的最顶层节点。
• 叶子节点(leafNode): 没有子节点的节点，即左、右节点全部为空(null)。
• 边(edge): 连接两个节点的线段，即节点的引用。
• 节点所在的层级(level): 根节点层级为1，从顶至底递增。
• 节点的度(degree): 节点的子节点数量，其中范围为0, 1, 2。分别表示没有子节点，即叶子节点；有一个子节点；有两个子节点。
• 节点高度(height): 从距离该节点最远的叶节点到该节点所经过的边的数量。
• 节点深度(Depth): 从根节点到该节点所经过的边的数量。
• 二叉树的高度(height): 从根节点到最远叶节点所经过的边的数量。

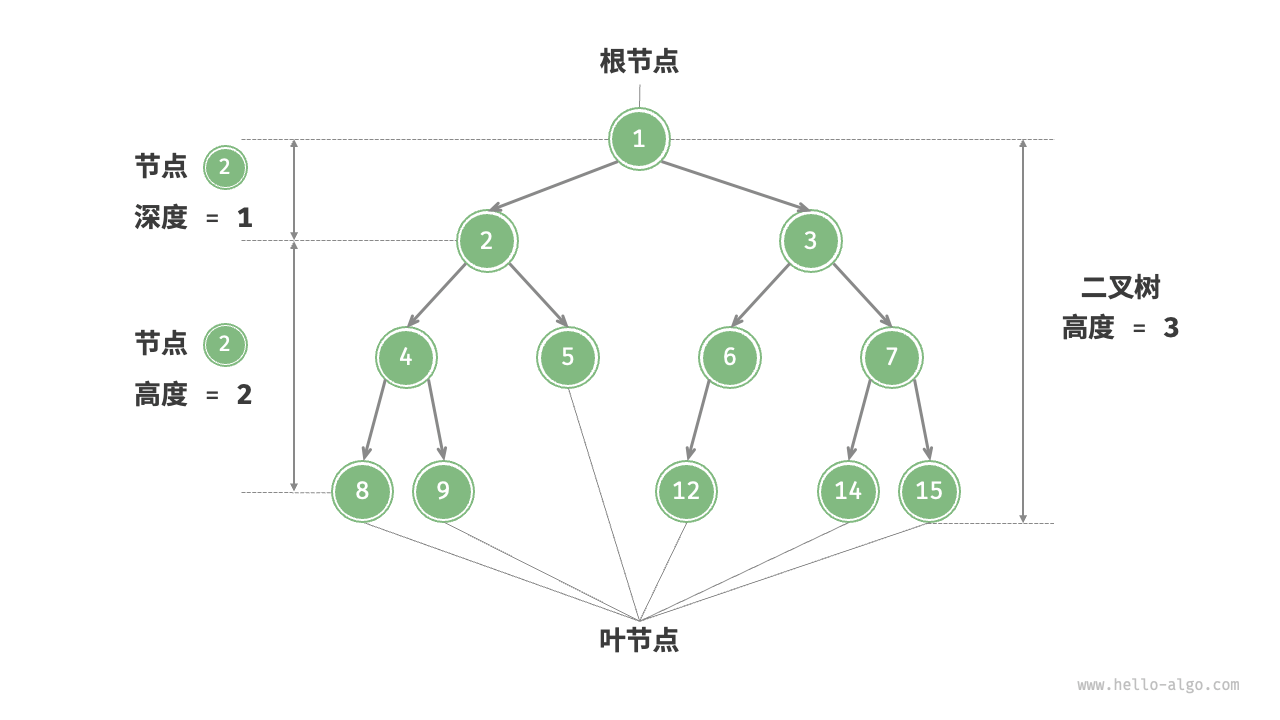
二叉树的常见类型

完美二叉树

完美二叉树：是指二叉树中所有层的节点都被填满，既除叶子节点的度为0，其它节点的度全部为2。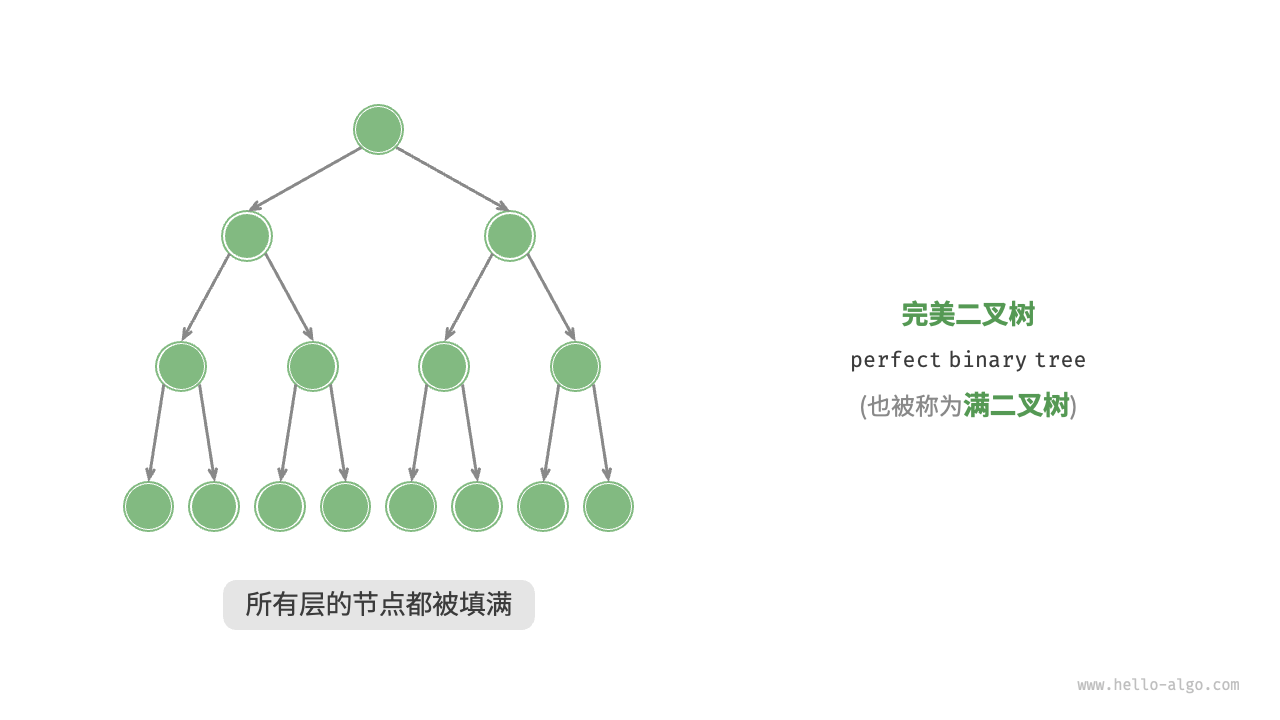

完全二叉树

完全二叉树：是指只有最底层节点未被填满且最底层节点尽量靠左填充。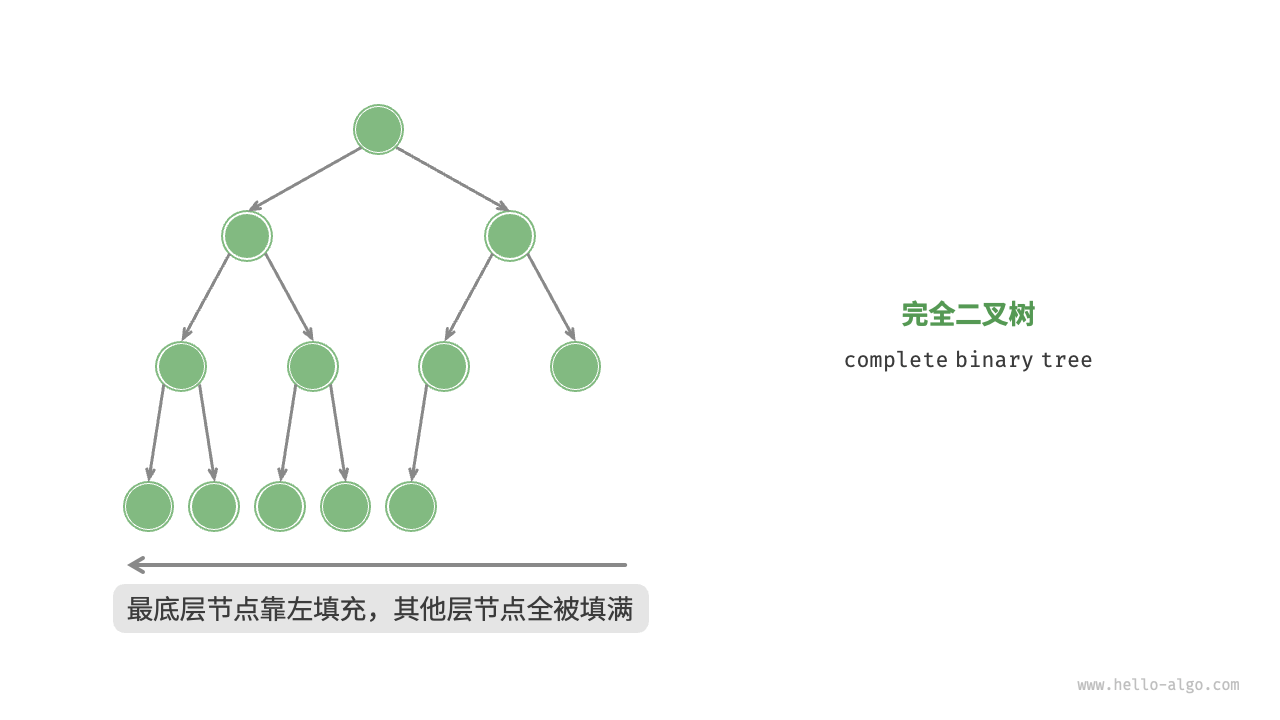

完满二叉树

完满二叉树：是指除叶子节点以外，其它节点都有两个子节点。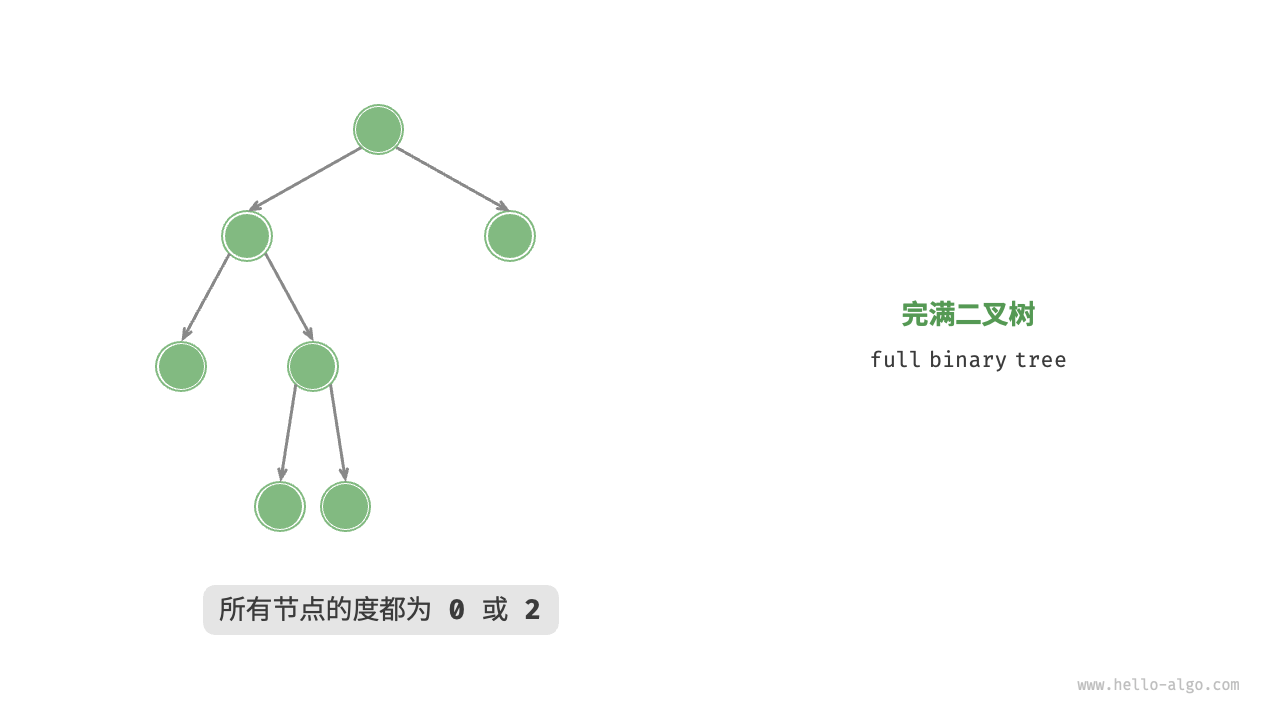

平衡二叉树

平衡二叉树：是指二叉树中任意节点的左子树的高度和右子树的高度只差的绝对值不超过1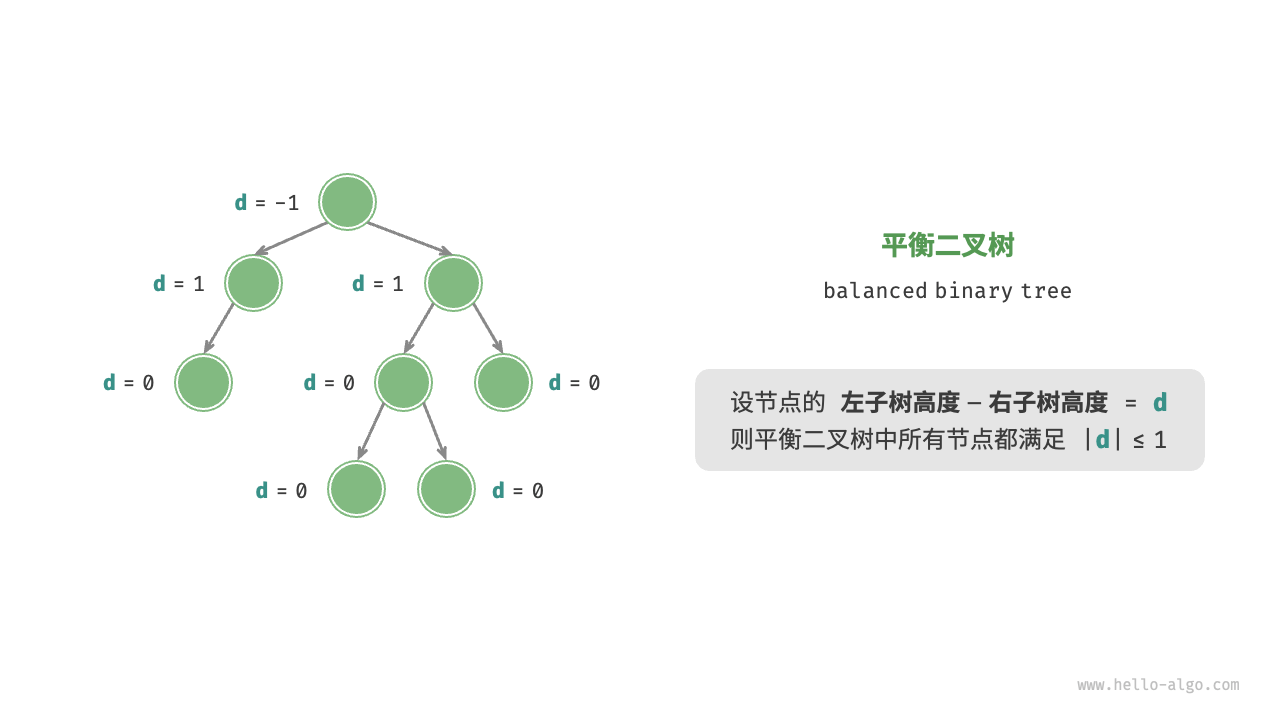

二叉树的遍历

二叉树常见的遍历方式包括：层序遍历、前序遍历、中序遍历和后序遍历。

层序遍历

层序遍历：是指从顶部到底部逐层遍历二叉树，并在每层中从左到右访问节点。层序遍历的本质是广度优先遍历BFS，它体现了一圈一圈向外扩散的逐层遍历方式。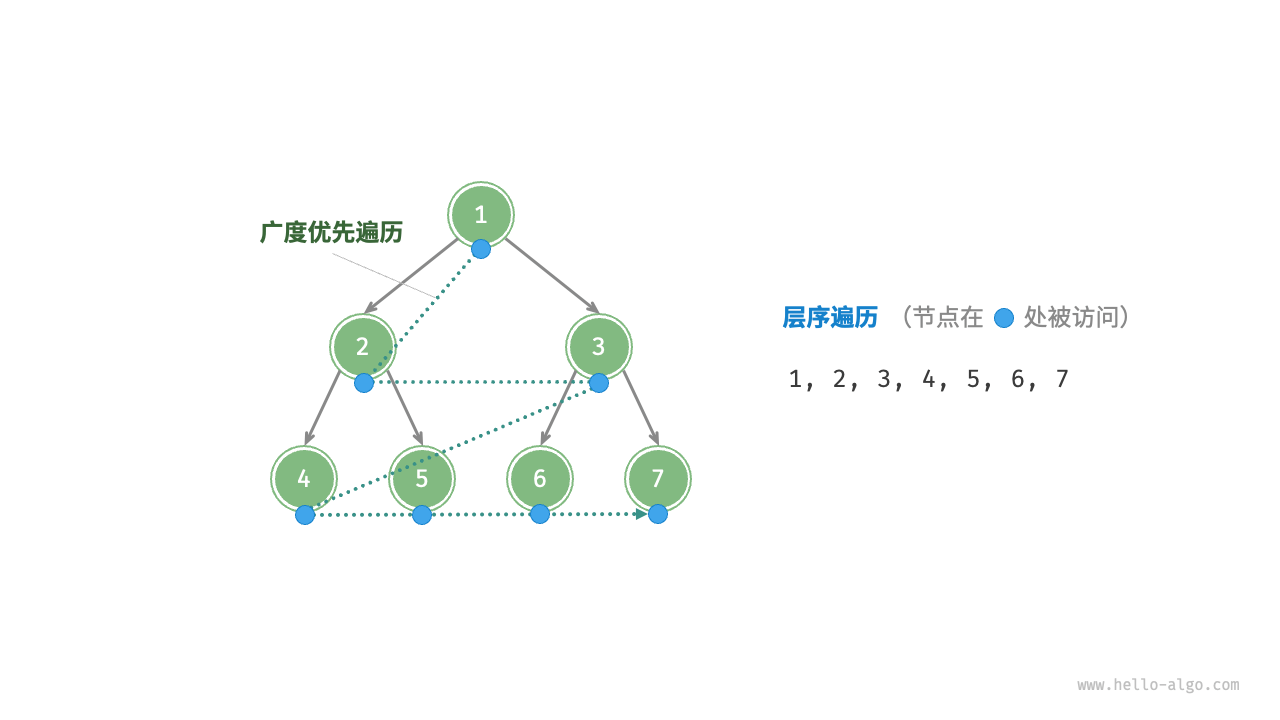

广度优先遍历通常需要借助队列来实现，因为队列遵循先进先出的原则。

// 层序遍历
// n为节点的数量
// 时间复杂度：O(n)，所有节点都需要遍历一遍
// 空间复杂度：O(n)，最坏的情况下，二叉树为完美二叉树，队列中存在最多同时存在(n + 1) / 2个节点。 
function levelOrder(root) {
  if(root === null) {
    return [];
  }
  const queue = [root];
  const list = [];
  while(queue.length) {
    let node = queue.shift();
    list.push(node.val);
    if (node.left) {
      queue.push(node.left);
    }
    if (node.right) {
      queue.push(node.right);
    }
  }
  return list;
}

前、中、后序遍历

与层序遍历相对的，前、中、后序遍历方式都属于深度优先遍历DFS，它体现了先走到尽头，再回溯继续的遍历方式。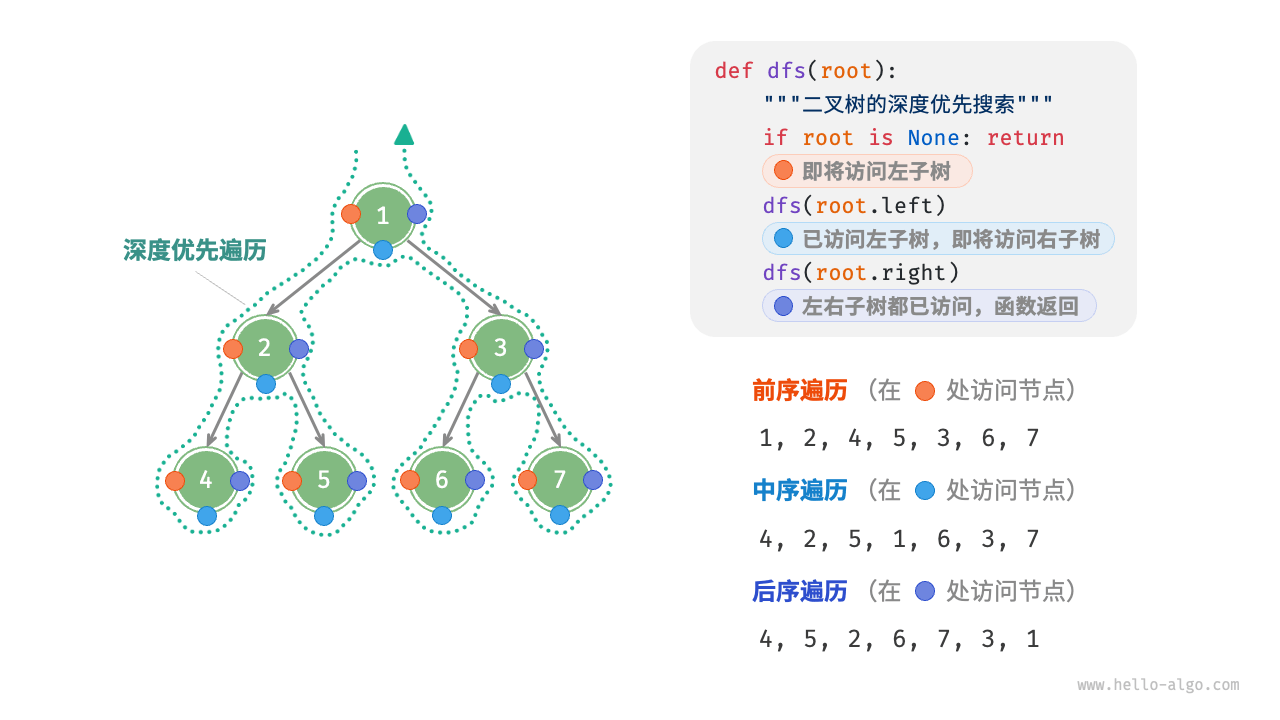

// n为节点的数量
// 时间复杂度：O(n)，需要遍历一遍所有节点
// 空间复杂度：O(n)，最坏的情况下，二叉树退化成一个链表，n为调用栈的内存开销。

// 前序遍历：根节点 => 左节点 => 右节点
function preOrder(root) {
  if (root === null) {
    return;
  }
  list.push(root.val);
  preOrder(root.left);
  preOrder(root.right);
}

// 中序遍历：左节点 => 根节点 => 右节点
function inOrder(root) {
  if (root === null) {
    return;
  }
  inOrder(root.left);
  list.push(root.val);
  inOrder(root.right);
}

// 后序遍历：左节点 => 右节点 => 根节点
function postOrder(root) {
  if (root === null) {
    return;
  }
  postOrder(root.left);
  postOrder(root.right);
  list.push(root.val);
}

二叉树的数组实现

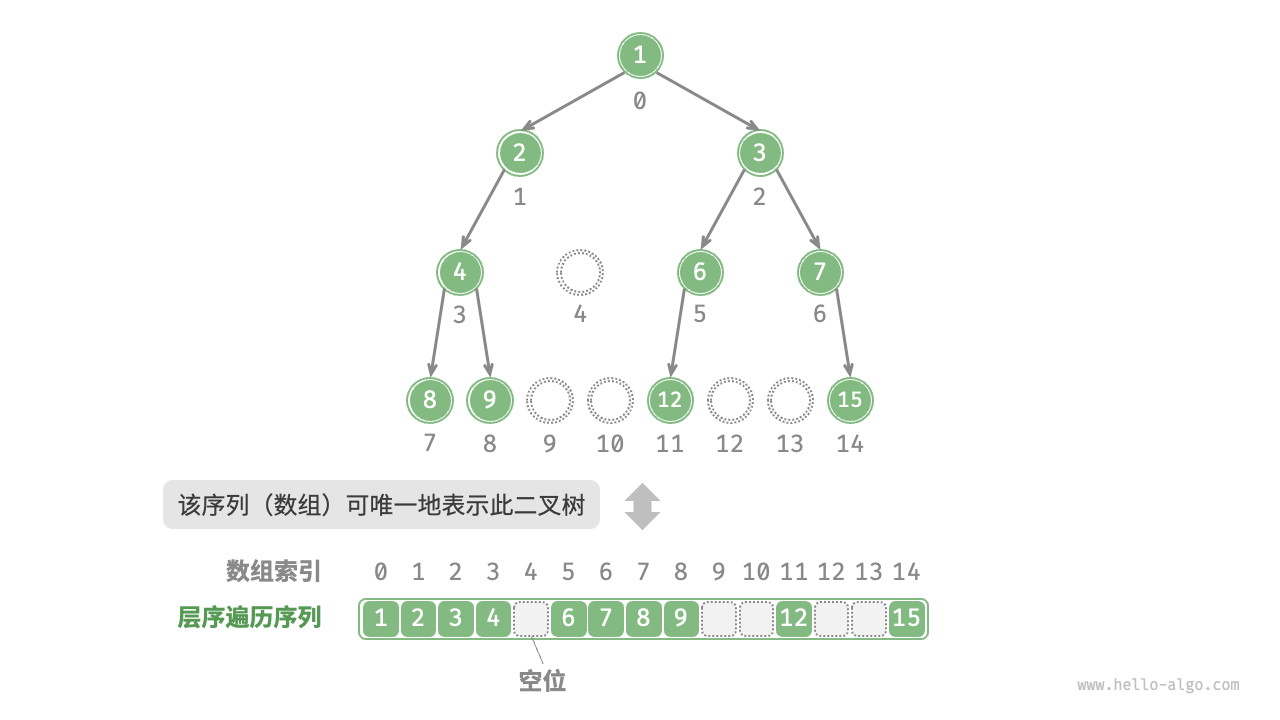
假设我们用一个层序结构的数组来表示下面这个二叉树：

// 为null表示没有此节点
let tree = [1, 2, 3, 4, null, 6, 7, 8, 9, null, null, 12, null, null, 15];

则我们可以实现基于数组的二叉树实现，其属性和方法如下：

• levelOrder(): 层序遍历。
• preOrder(root)：前序遍历。
• inOrder(root)：中序遍历。
• postOrder(root): 后序遍历
• dfs(i, order, res)：深度优先遍历，前、中、后序遍历的实现基础。
• size(): 获取二叉树的节点数量。
• val(i): 获取索引为i节点的值。
• left(i): 获取索引为i节点的左节点的索引。
• right(i)：获取索引为i节点的右节点的索引。
• parent(i)：获取索引为i节点的父节点的索引。

完整实现代码，请参考二叉树的数组表示

优点和局限性：

• 数组存储在连续的内存空间中，对缓存友好，访问与遍历速度较快(优)，但不适合存储数据量过大的树(缺)。
• 不需要存储指针，比较节省空间(优)。
• 允许随机访问节点(优)。
• 增删节点需要通过数组插入与删除操作实现，效率较低(缺)。
• 当二叉树中存在大量空节点时，数组中包含的节点数据比重较低，空间利用率较低(缺)。

二叉搜索树

二叉搜索树需要满足如下几个特点：

1. 对于根节点，左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值。
2. 任意节点的左、右子树也是二叉搜索树，即满足条件一。

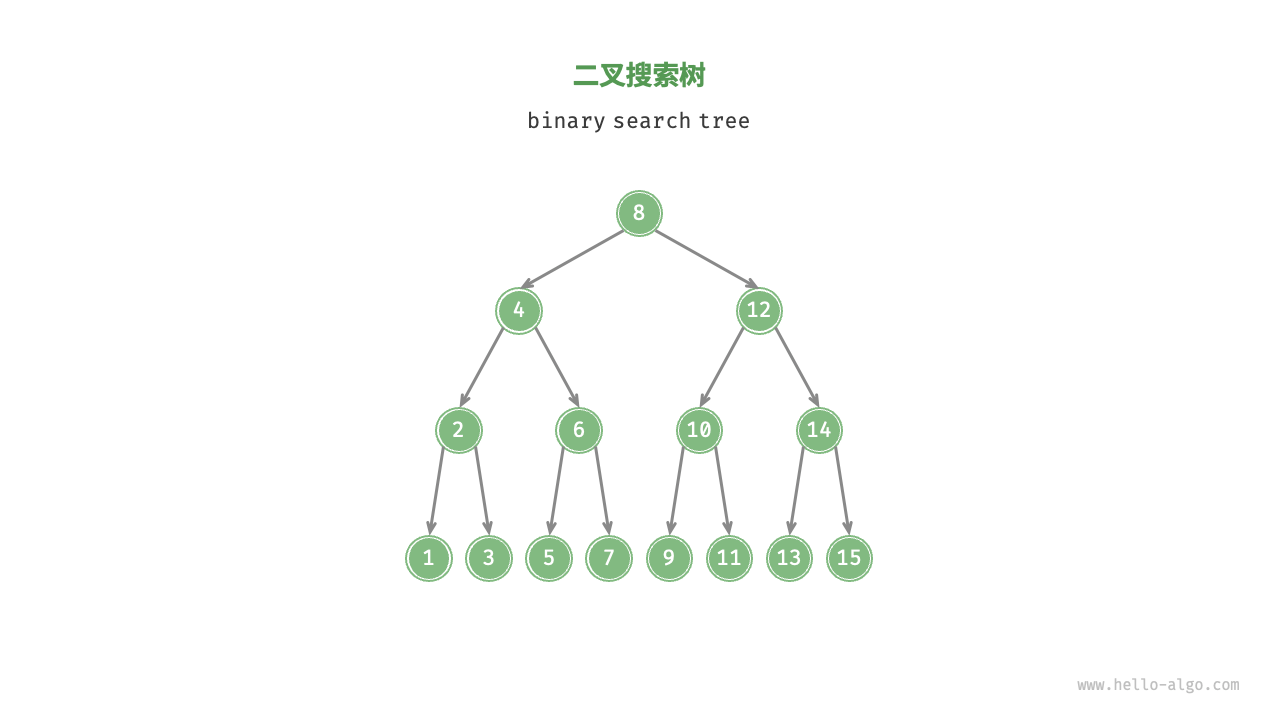
二叉搜索树的实现

根据二叉搜索树的特性，需要实现如下几个方法：

• search(val): 在二叉树中根据值查找节点。
• insert(val): 在二叉树中插入一个新节点，如果已经存在则不执行插入操作。
• remove(val): 在二叉树中删除一个节点，如果节点不存在则不执行删除操作。
• levelOrder()：层序遍历，根据层序遍历的特点和二叉搜索树的特性，层序遍历返回的节点是升序的。
• preOrder()：先序遍历。
• inOrder()：中序遍历。
• postOrder()：后序遍历。
• minNode()：最小值节点。
• maxNode()：最大值节点。

二叉搜索树的完整实现，请参考二叉搜索树的实现

二叉搜索树的效率

基于二叉搜索树的特性，其各项操作的时间复杂度都是对数阶，具有稳定且高效的性能。它和数组的效率对比如下：

操作	数组	二叉树
查找元素	O(n)	O(logn)
插入元素	O(1)	O(logn)
删除元素	O(n)	O(logn)

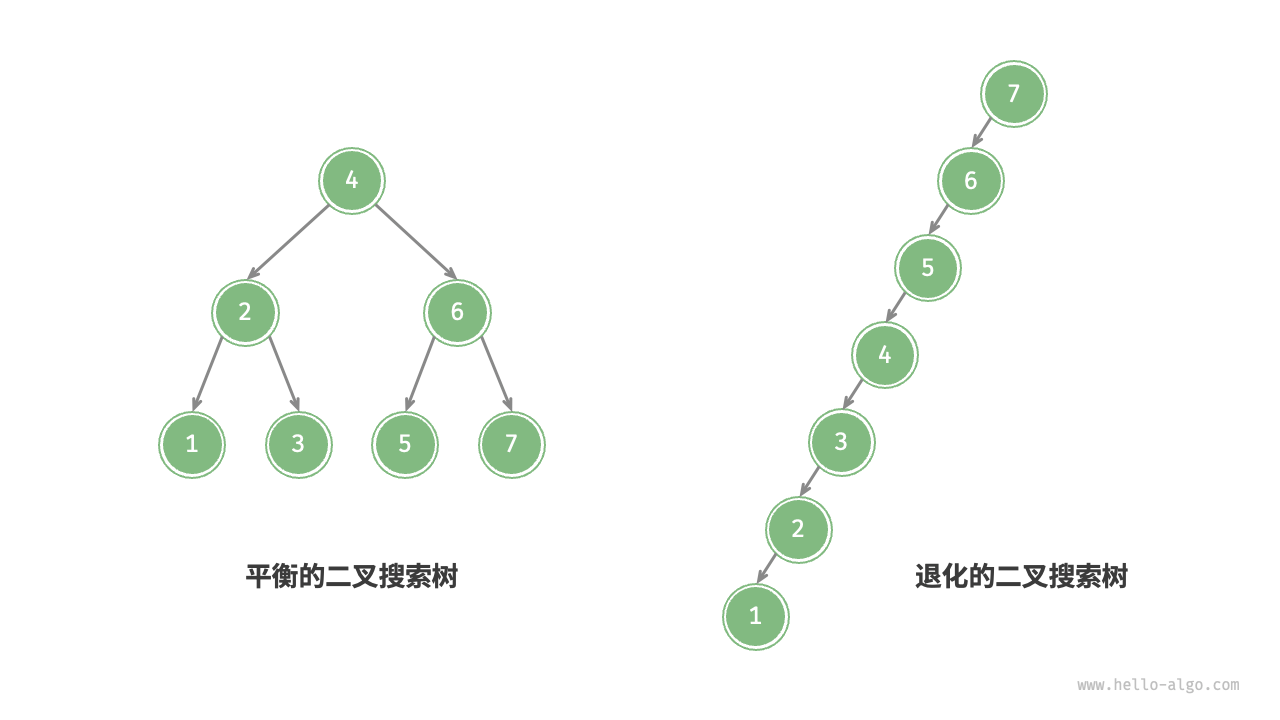
在理想情况下，二叉搜索树是平衡的，但如果不断地插入和删除元素节点，则二叉树会退化成链表，此时效率退化为O(n)。

二叉搜索树的应用

• 用作系统中的多级索引，实现高效的查找、插入、删除操作。
• 作为某些搜索算法的底层数据结构。
• 用于存储数据流，以保持其有序状态。

AVL树

参考

• Hello 算法 树
• JavaScript 数据结构和算法 二叉树章节